Continue to Site

Eng-Tips is the largest engineering community on the Internet

Intelligent Work Forums for Engineering Professionals

Register Log in
  • Congratulations KootK on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!

Pushover analysis of a metallic structure

Status
Not open for further replies.
Ossau56

Ossau56

Civil/Environmental
Jan 11, 2023
7
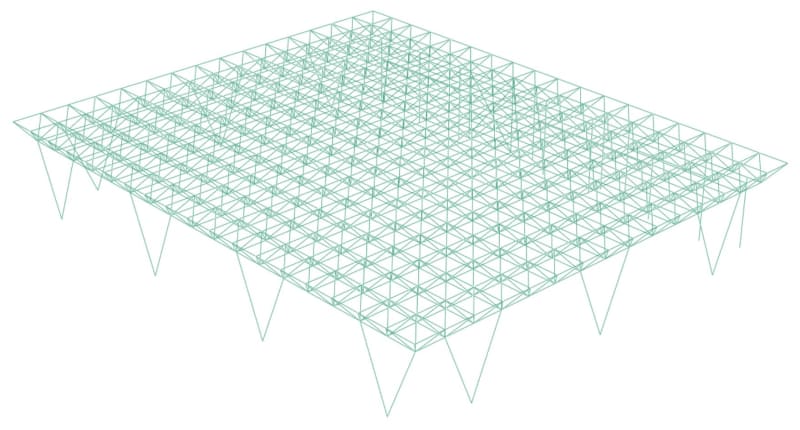
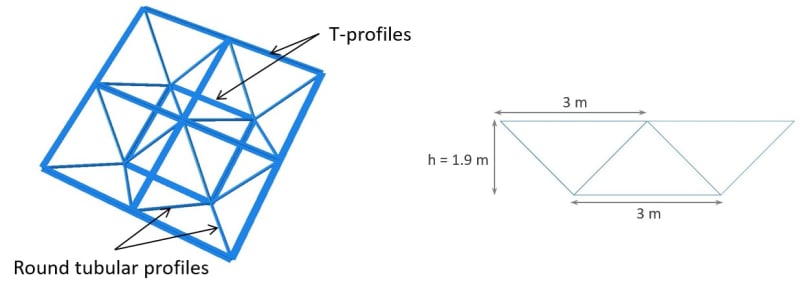
I’m modeling a metallic structure whose roof collapsed under snow weight. I modeled this structure using beam elements and I specify that the roof elements are bolted together (no ball joint).
The calculation is made in static and the snow loading is applied using linear forces.
In small displacements, the code diverges while I have not reached the steel ultimate strength; I get the following error message: “The strain increment is so large that the program will not attempt the plasticity calculation at 171 points. The plasticity/creep/connector friction algorithm did not converge at 55 points.” I tried to increase the time period, to decrease the initial and minimum increment sizes, to increase AI or to reduce the size of the mesh… Nothing works! And in big displacements, the code diverges even earlier! As a result, I can’t perform risk analysis integrating imperfections.
I would appreciate a recommendation on how to improve convergence in small and big displacements?
 
Sounds like you need larger Iy.
What's the frame look like?

Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
what code are you using?
what material properties are you using? are they minimum properties, or realistic typical properties?
perhaps the joints in the model are more flexible than the real structure.(?)
if the roof collapsed, why do you expect your model to converge?
 
Thank you for your response.
I'm using Abaqus.
I'm using an elasto-plastic law with next properties : E=210MPa,fy=294MPa,fu=432MPa and epseu=0.2.
I don’t necessarily expect my model to converge but the error message is not clear. I can’t know if the code is diverging because the structure collapses or because there’s a numerical convergence problem.
 
Try with it only dead load, element weight only.
Depth of the trusses looks too small.
Some dimensions would help.

Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
If you lessen the loads will it run?
Software error messages that are 100% correct but totally useless are a fact of life.

= = = = = = = = = = = = = = = = = = = =
P.E. Metallurgy, consulting work welcomed
 
I have a first step with only dead load that goes well.
The building is 54 m long, 45 m wide and 8.9 m high. You will find attached a description of one single roof frame element; the outside and inside diameters of the tubes are 48.30 mm and 42.5 mm respectively.
 
 https://files.engineering.com/getfile.aspx?folder=90046b88-6b79-4228-b3af-7258d18256a6&file=RoofFrameElementDimensions.png
Capture2_lfflud.jpg

RoofFrameElement_fejkvr.jpg


Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
The forces in the top and bottom chords will be very high.
I suspect they are failing with full load.

What loads are you using and
What is the material's yield strength?

1.9m depth of truss is probably half of what you will need to control deflection.

Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
I'm using line loads and the material's strength is 294 MPa.
 
N/m^2 ?

Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
Just did a very quick check of forces generated at midspan assuming one way action.
Using a very minimal total load of 500 N/m2 (10 psf), trusses fail generating 2 x Yield Stress.
If the roof acted as a rigid plate, lets say you can carry load in both directions, roughly dividing the stress by 2. So that system most likely fails with about a 500 N/m2 load.

Hope it doesn't snow. Its barely carrying its own weight.



Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
I'm using an elasto-plastic load with an ultimate strength equal to 432 MPa.
 
Won't work.

Too much stress in the fibres.

Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
N/m^2 is the definition of Pascal, not MPa. 294 MPa is about 42 ksi.
 
Engineering Toolbox uses N/m2 for roof loads.
I use Pa for fluid pressure and stress.

The 500 N/m2 roof load produces 42ksi member stress.

Screenshot_20230113-074139_Brave_wrkqwy.jpg


Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
I have never used 'Engineering Toolbox', but those of us who deal everyday in SI for structural purposes use kN loads, kPa distributed load, kN/m line loading, MPa stress. We rarely use N or Pa alone, but instead use the derived units. That's just the way we think.
 
Right. But I think you calculate kM/m line load by multiplying N/m2 x C/C spacing and dividing by 1000? In the States its a floor or snow load in, psf, x C/C ft = lbs_force/ft /1000 for Kips_lineal l_ft.

Einstein gave the same test to students every year. When asked why he would do something like that, "Because the answers had changed."
 
Status
Not open for further replies.

Similar threads

L
  • Question
Buckling Analysis Help
Replies
4
Views
2K
dik
dik
T
  • Question
Thermal load with thermal gradient in structural analysis
Replies
6
Views
621
Amp Dylan
A
B
  • Question
Design of Simple Lift beam with a trolley
Replies
5
Views
3K
dvd
dvd
eng_saad
  • Question
creep of conductor
Replies
0
Views
1K
eng_saad
eng_saad
Blackfairy
  • Question
Design of Asphalt Pavement without Subbase
Replies
7
Views
4K
fel3
fel3

Part and Inventory Search

Sponsor

Back
Top Bottom