Question : Rotation Direction of Harmonics. Why some CW and some CCW in 3 phase induction motor?
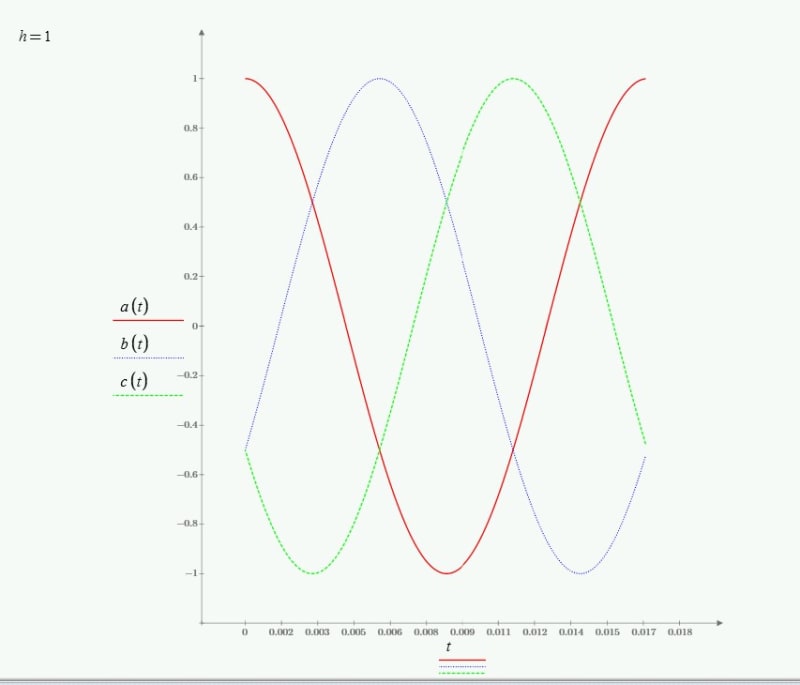
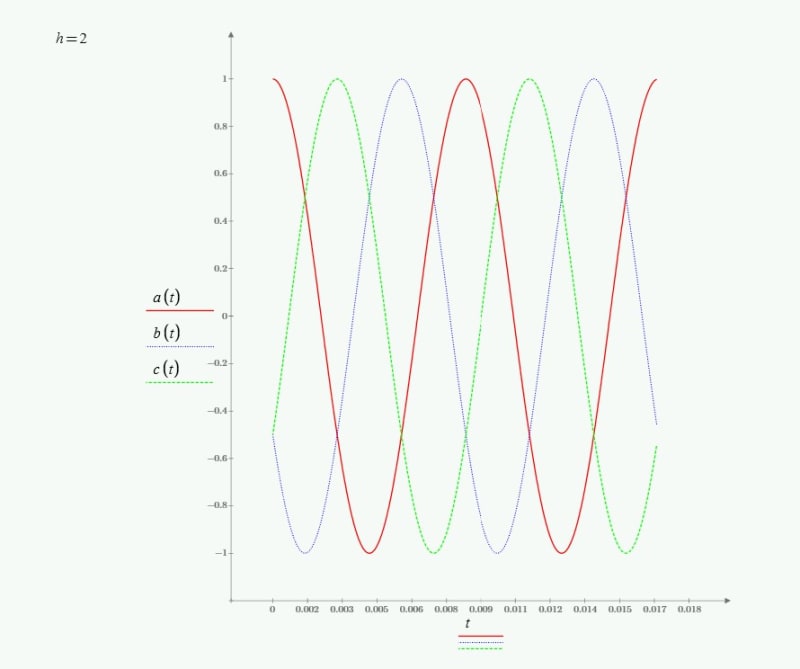
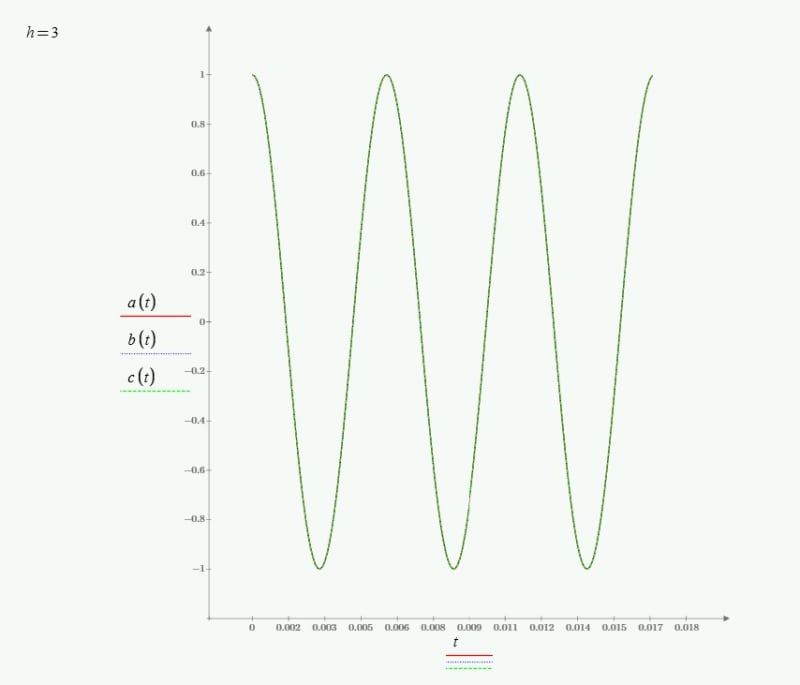
Assuming with A-B-C phasor sequence, a 3 phase induction motor field rotates clockwise. Assuming the motor has 4 poles, speed will be just under 1800 rpm clockwise for 60hz supply. If we decrease frequency, the motor will slow down and if we increase frequency, the motor will speed up, in the same direction. I have difficulty understanding that for 2nd harmonic, meaning at 120hz, the field rotates in opposite direction.
I am looking for some simple explanation (Not too much mathematics) to understand why 2nd harmonic (and some other harmonics) rotate in opposite direction in the motor.
I do understand the positive, Negative and zero sequence components at fundamental frequency and also it is clear that if we switch any two supply terminals of induction motor, it will rotate in opposite direction. The question is specific to 2nd harmonic (120 hz) which may have small magnitude, but why opposite direction to fundamental frequency rotation, when no terminals have been switched ?
Thanks.
Assuming with A-B-C phasor sequence, a 3 phase induction motor field rotates clockwise. Assuming the motor has 4 poles, speed will be just under 1800 rpm clockwise for 60hz supply. If we decrease frequency, the motor will slow down and if we increase frequency, the motor will speed up, in the same direction. I have difficulty understanding that for 2nd harmonic, meaning at 120hz, the field rotates in opposite direction.
I am looking for some simple explanation (Not too much mathematics) to understand why 2nd harmonic (and some other harmonics) rotate in opposite direction in the motor.
I do understand the positive, Negative and zero sequence components at fundamental frequency and also it is clear that if we switch any two supply terminals of induction motor, it will rotate in opposite direction. The question is specific to 2nd harmonic (120 hz) which may have small magnitude, but why opposite direction to fundamental frequency rotation, when no terminals have been switched ?
Thanks.