Tek-Tips is the largest IT community on the Internet today!
Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!
-
Congratulations TugboatEng on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
Vertical Pipe Flow
- Thread starter Bumblyari
- Start date
LittleInch
Petroleum
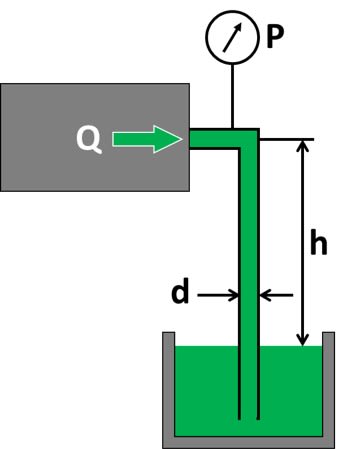
So long as the pipe is full it doesn't matter if the pipe is up, down or flat.
Define your question better and add some drawings.
Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
Define your question better and add some drawings.
Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
- Thread starter
- #3
LittleInch
Petroleum
The issue in something like that which is open to atmosphere is that the pressure drop in height h is usually more than the frictional losses unless you're flowing at a very fast velocity.
So if the negative number you get from your calculation is too high, the fluid vaporises at the top point / the pressure falls to less than atmospheric pressure.
Flow down vertical pipes is a world of its own and you normally need the Froude number to be less than 0.3 (I think)
But maybe if you explain why you're asking you can get a better answer.
Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
So if the negative number you get from your calculation is too high, the fluid vaporises at the top point / the pressure falls to less than atmospheric pressure.
Flow down vertical pipes is a world of its own and you normally need the Froude number to be less than 0.3 (I think)
But maybe if you explain why you're asking you can get a better answer.
Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
- Thread starter
- #5
LittleInch
Petroleum
Basically what you need is the smallest pipe where the frictional head losses in length of pipe h (actually h plus the length under the liquid level) at flow rate Q for viscosity V are lower than the head difference h. Note it's the pipe total length here that counts so if there are any horizontal bits, they count as well
So for different fluid viscosities you can usually either find a chart or calculate head loss for your length h. As you go down in size for the same Q the head loss goes up quite dramatically as you get smaller and smaller.
Does that make sense?
Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
So for different fluid viscosities you can usually either find a chart or calculate head loss for your length h. As you go down in size for the same Q the head loss goes up quite dramatically as you get smaller and smaller.
Does that make sense?
Remember - More details = better answers
Also: If you get a response it's polite to respond to it.
- Thread starter
- #7
- Status