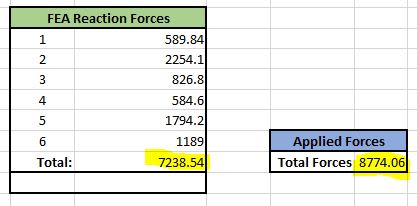
Hi Everyone,
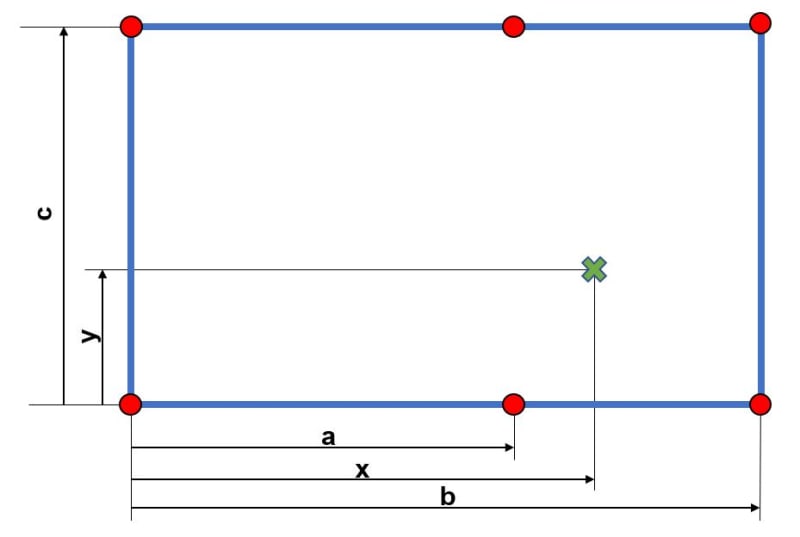
I have a structure supported by six legs that are bolted to the floor. The top view of this setup is shown below. The center of gravity of this structure is marked with a green X, the fixed support legs are shown with red points. I would like to work out the force exerted on the floor by each leg.
x is bigger than a but smaller than b.
What is the best way to approach this problem?
I have tried to derive an equation for this but as you can guess, I didn't have any luck.
I understand that I could go down on the FEA route but what I would like to get out this is an equation system that I can use in Excel when the numbers change.
Many thanks for your help.
I have a structure supported by six legs that are bolted to the floor. The top view of this setup is shown below. The center of gravity of this structure is marked with a green X, the fixed support legs are shown with red points. I would like to work out the force exerted on the floor by each leg.
x is bigger than a but smaller than b.
What is the best way to approach this problem?

I have tried to derive an equation for this but as you can guess, I didn't have any luck.
I understand that I could go down on the FEA route but what I would like to get out this is an equation system that I can use in Excel when the numbers change.
Many thanks for your help.