"I just wanted to have a feel or a sense of how this global buckling load is obtained/derived. How is this global buckling capacity is different from local individual member buckling capacity? "
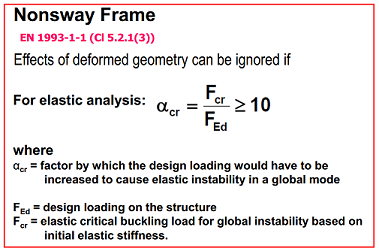
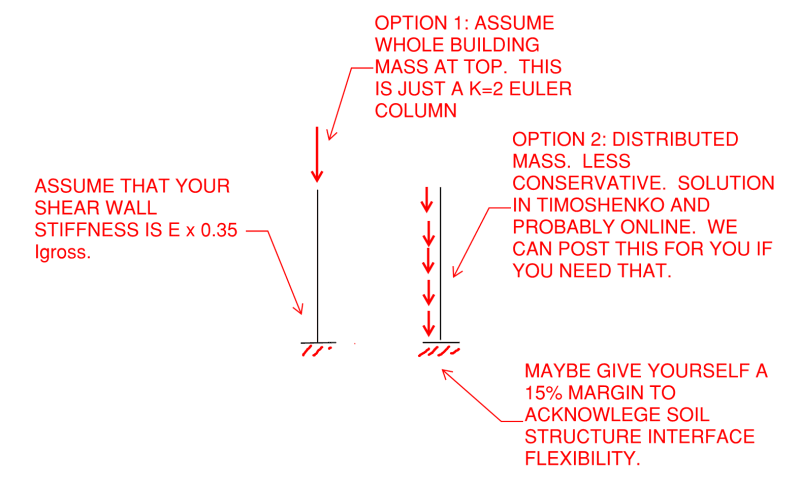
The global buckling load is often obtained by solving an eigenvalue problem; implicit assumptions include zero transversal forces (only axial loads). This can be done with FEM-software for almost any geometry, or for simple geometries (frames in a plane) with FEM by hand or with Berry´s stability function approach. A more exact solution is given by applying large deflection theory (equilibrium equations formulated in deformed shape, with large displacements and moderate rotations), solving the non-linear problem iteratively (which produces a force vs. deflection curve), and recognizing at what load level the deflection and stress start to increase dramatically.
Local, individual member buckling capacity is what you described it as: local and for an individual member, whose stiffness properties is not affected by other members - think of them as your classical Euler column cases. Such columns are not always used, and indeed, if you have a frame structure, the buckling capacity is a function of all member lengths, stiffnesses, joint types and the boundary conditions. Therefore, the global buckling capacity depends on many members.
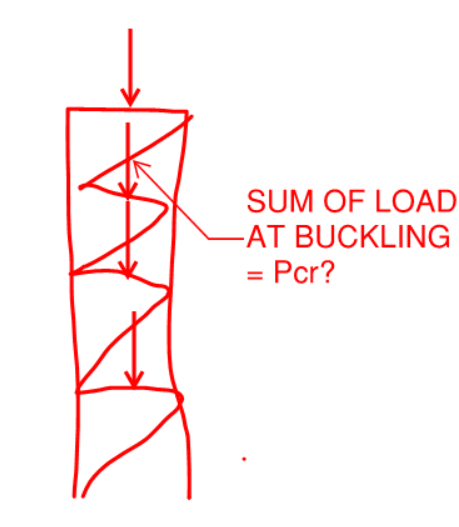
"Wouldn't one column buckling at the lowest floor cause global instability? or does the load redistribute to other members? A few members buckled at global buckling modes? sadeyes

"
The buckling tendency is a function of all members in a frame structure. If you have slender columns on the lowest floor and stiff members on the upper floors, and large axial loads are transferred to the first floor, you will of course see the first mode of failure occurring as the buckling of the slender column.


![[sadeyes] [sadeyes] [sadeyes]](/data/assets/smilies/sadeyes.gif)
![[smile] [smile] [smile]](/data/assets/smilies/smile.gif)