Tek-Tips is the largest IT community on the Internet today!

Members share and learn making Tek-Tips Forums the best source of peer-reviewed technical information on the Internet!

Register Log in
  • Congratulations cowski on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!

Beam deflection problem with multiple Uniformly Distributed Loads

Status
Not open for further replies.
everydayengineer

everydayengineer

Student
Joined
Aug 7, 2021
Messages
2
Location
US
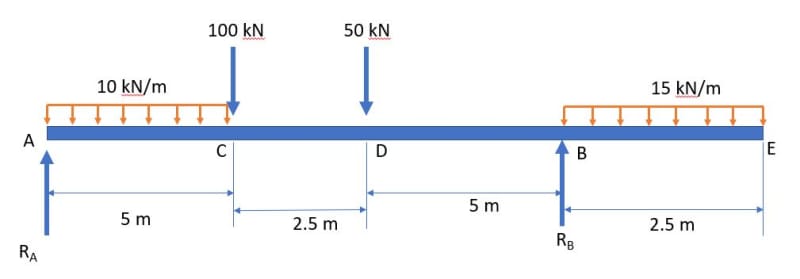
Capture_eyxcwt.jpg


Hi all,

I am trying to solve this beam problem to find the deflection at different points along the length of the beam. However I am having a hard time writing the equation for bending moment using Macaulay's theorem since there are 2 uniformly distributed loads of different magnitudes.

Can someone help solve this problem?

Thank you in advance!
 
Sort by date Sort by votes
Your structure is statically determinate, so you can solve for RA and RB directly. From there, you can find the moment at any point distant 'x' from Point A using simple statics.

Macaulay's Theorem is just another name for the Double Integration Method. I was going to refer you to the following for a simple example of a beam with a point load at midspan. Unfortunately, the man in the video gets the expression for dy/dx (slope) and y (deflection) wrong. Can you find his error?


Personally, I would not use the Macaulay Theorem to solve this problem, unless you are required to use it in your assignment. There is nothing wrong with the method, but with that many loads, it is very easy to drop a term or make some arithmetic error. There are a number of easier ways to solve it. One method would be to treat each load separately, then use superposition to find the combined answer for slope and deflection at any point distant 'x' from Point A.

We can't solve your problem for you, but it really is pretty straightforward, even though it has a lot of terms. Start by solving for the two reactions, then express the moment at any point distant 'x' from Point A and show us what you've got.

BA
 
Upvote 0 Downvote
There is not a one-equation continuous solution. There are four (4) equations needed. One of the 4 equations will be valid within each range between loading conditions.

 
Upvote 0 Downvote
1503-44 said:
There is not a one-equation continuous solution. There are four (4) equations needed. One of the 4 equations will be valid within each range between loading conditions.
Click to expand...
Correct, although there are similarities in the equations, some having additional terms accounting for different ranges. That point was missed by the instructor in the video which I mentioned earlier. He used the wrong expression when finding the slope at Point A and came up with the wrong answer. (see below)

image_x7aofg.png


Although he came up with the correct answer for deflection at midspan, his expression for deflection was not valid for the left half of the beam.

BA
 
Upvote 0 Downvote
If boolean expressions are used, a single equation can be written for the whole span.

Mx = RA.x - P(x-a)(x>a) - Q(x-b)(x>b) - R(x-c)(x>c)​

is the moment at any point of a simple span beam, distant x from Point A, with point loads P, Q and R at a, b and c respectively from Point A. The boolean expressions, shown in red have the value of 1 or 0 depending on whether the bracketed expression is true or false.

BA
 
Upvote 0 Downvote
I was confusing myself thinking I could write one nice complete moment equation that would tell me the deflection at any point. but that is wrong because the bending behavior differs at each section of the beam.

I was actually able to write moment equations for individual sections and integrated them twice(which ended up with a lot of constants of integration - 8 in total). Then I applied multiple boundary conditions to solve for all the constants. boundary conditions were:
1. deflection = 0 at supports - (solved for 3 constants).
2. deflection is the same at a particular point, meaning I could equate the deflections given by 2 different equations (points C and D) - (solved for 2 constants).
3. slope is the same at a particular point, meaning I could equate the slopes given by 2 different equations (points C, D and B) - (solved for 3 constants).

Thus I now have different bending moment, slope and deflection equations for different sections of the beams!

thank you all for the great inputs :)
 
Upvote 0 Downvote
Happy to hear you found the solution. Congrats!

BA
 
Upvote 0 Downvote
BAretired,

I was taught to write equations like that as...

Mx = RAx - P<x-a> - Q<x-b> - R<x-c>,​

with the pointy brackets being zero if the contained value was equal to or less than.

--
JHG
 
Upvote 0 Downvote
Okay, that is clear and easier to write. I have not run into that notation until now, but it makes sense.

BA
 
Upvote 0 Downvote
Status
Not open for further replies.

Similar threads

lambosan16
  • Locked
  • Question Question
ABAQUS: Loads on multiple points, single body
Replies
2
Views
639
lambosan16
lambosan16
Galbert99
  • Question Question
problem with cyclic region of a gear in ansys mechanical
Replies
4
Views
4K
Galbert99
Galbert99
L
  • Locked
  • Question Question
deflection limits
Replies
5
Views
5K
LKkk
L
H
  • Locked
  • Question Question
Problem with device (sound to electrical energy)
Replies
7
Views
4K
IRstuff
IRstuff
MyCupboard
  • Question Question
Multiple Sleeve holes in Concrete FDN Wall
Replies
4
Views
11K
MyCupboard
MyCupboard

Part and Inventory Search

Sponsor

Back
Top