Let me take a stab at this:
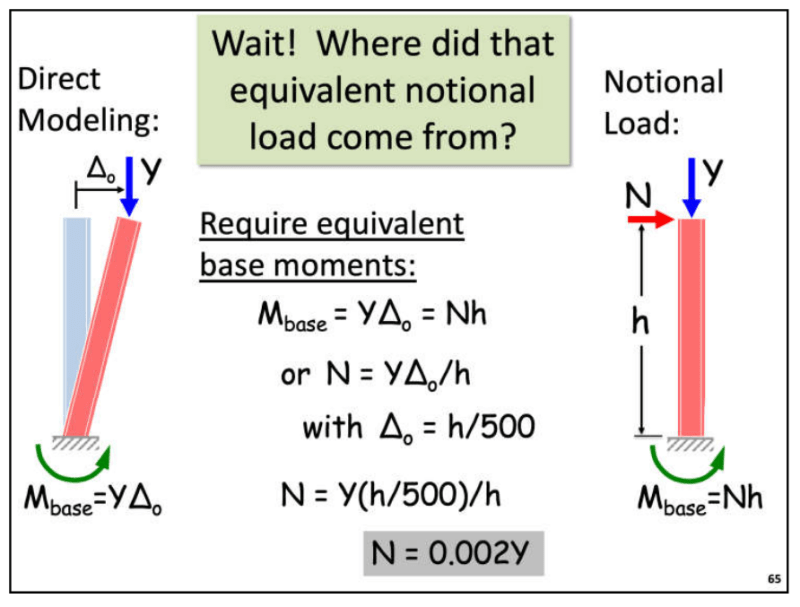
1) Derivation of Notional Load based on L/500 out of plumbness:
Ingenuity is correct about this in that the derivation of the 0.002 notional load (AISC section C2.2b, equation C2-1) is based on the L/500 out-of-plumbness and can be adjusted in cases where the use of a different out-of-plumbness is justified.
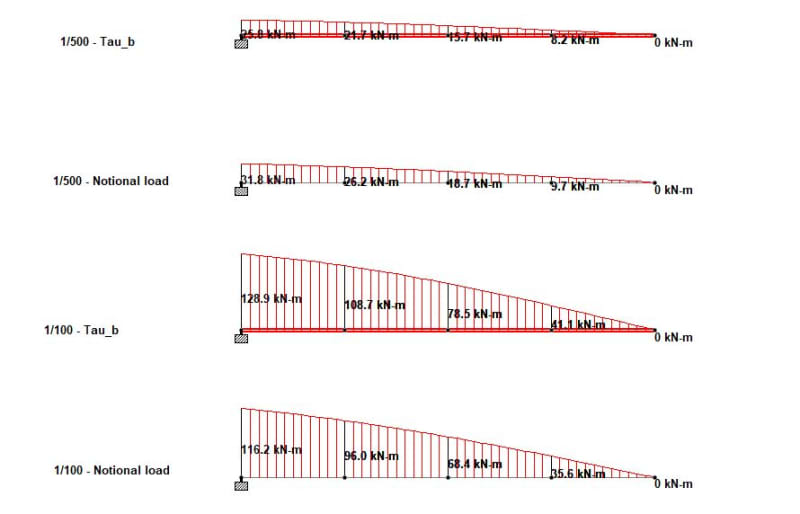
2) Purpose of Tau_b:
I don't believe JLNJ is quite correct when he asserts that Tau_b is related to the connection stiffness. Instead, it is an attempt to approximate the fact that most steel columns will experience INELASTIC buckling. Therefore, an analysis which captures geometric non-linearity (e.g. P-Delta) which does a good job of capturing elastic buckling would still not be sufficiently accurate to capture the behavior of most steel columns. That's why the Tau_b factor was introduced. I'm sure there are some good technical articles about this out there, but I don't have them off hand. I'd look for some co-authored by Don White (of Georgia Tech) between 1998 and 2005.
There were originally TWO Tau values, this is discussed in the commentary to section C2.3. One for intermediate or stocky columns (where inelastic buckling governed) and one for very slender ones (where elastic buckling governed).
3) The use of Notional Load to use a constant Tau_b:
This is based on section C2.3 where it says (paraphrasing), "it is permissible to use Taub = 1.0 if an additional notional load of 0.001*gravity loads is applied at all levels, in all load combinations".
Note that this applies to ALL load combinations, whereas the original notional loads only applied to gravity only load combinations (unless your 2nd order drift is quite high).
The purpose of this clause, I believe, was to allow a simpler design method for engineer who didn't want to (or couldn't) adjust the stiffness of their structural members based on axial load. That's really convenient because it allows for a non-iterative analysis.
To me, this 3rd item is the basis of the OP's original question and I don't have a great answer to how this was derived. I don't believe that there is anything in the code that would prevent him from using this in lieu of Tau_b if the out-of-plumbness were greater or less than L/500. Personally, I would use the 0.001 value for any out-of-plumbness that is less than L/500 and adjust it to 50% of the other notional load if out-of-plumbness were greater than L/500.
But, I would want to check my 2nd order amplification factor. If it is greater than 1.7, then I'd want to do the Tau_b adjustment.... Heck, if it were greater than 1.7, then I'd want to change my structure and stiffen it up!