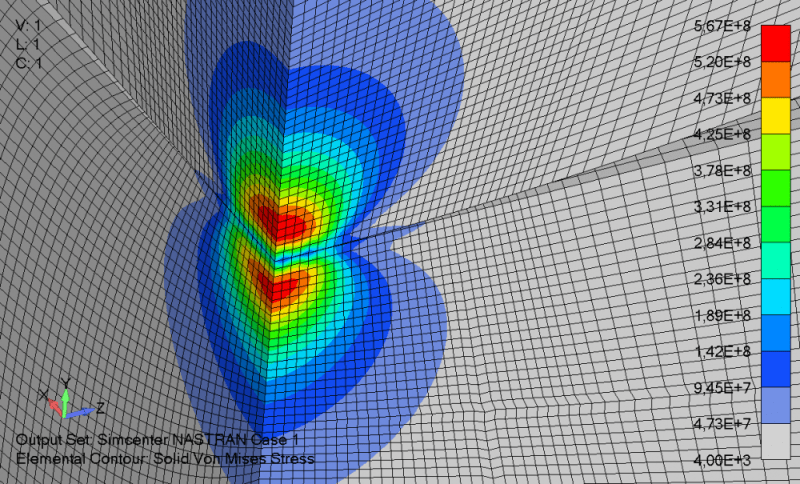
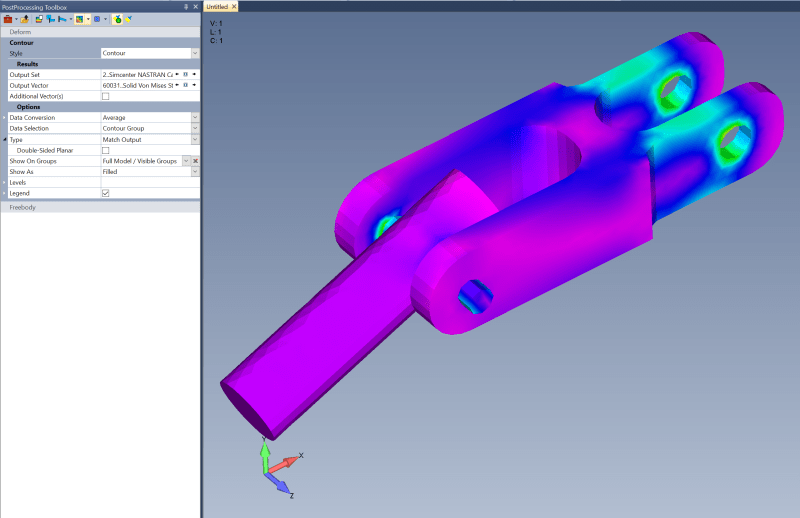
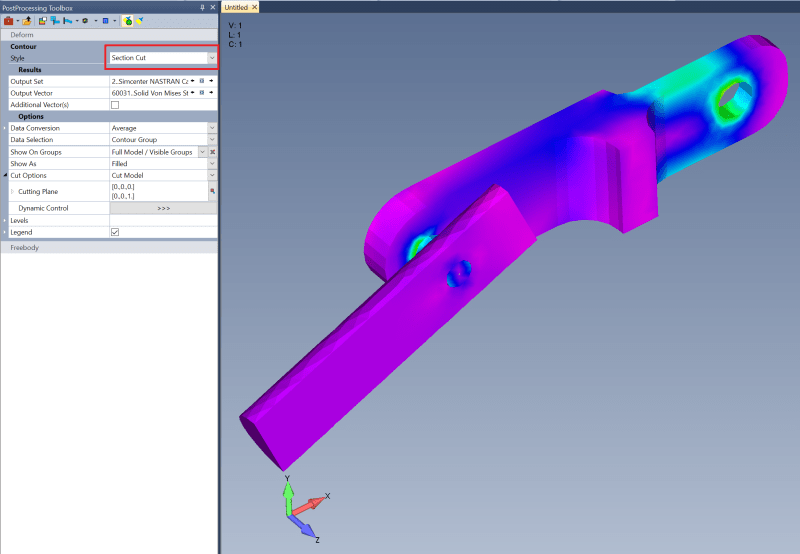
I am reading through a paper on mesh convergence created by ANSYS and they have pointed out something I have long wondered about FEMAP's solid refinement method using mesh by surface on the meshing toolbox. The basic claim by ANSYS is even though the surface mesh has been refined on a solid there can still be larger poorly shaped elements laying just under the surface that can cause errors in mesh discretization. I have worried about this is in FEMAP and have often figured out ways avoid using TET mesh and local refinement techniques and instead use a uniformly refined HEX mesh where possible, so I know exactly what type of element I am getting through the cross-section. However, sometimes this is not possible with complex geometry and I must mesh the piece with TET elements and due to computing power and time, I must refine locally near high-stress gradient regions. Can anyone help me understand if this is a real concern and if there are techniques I can use to avoid any errors caused by this if so?

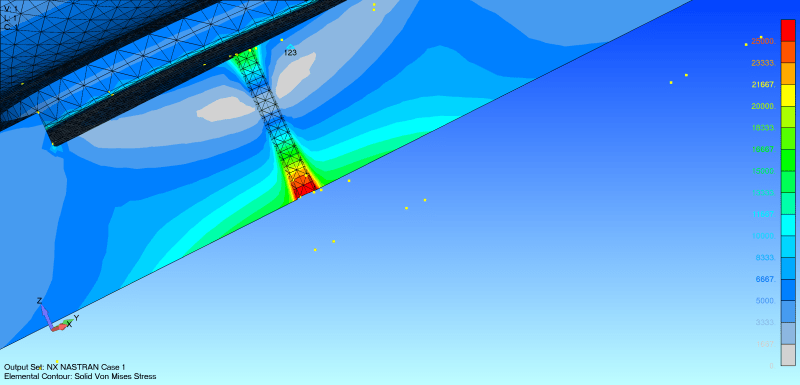
ANSYS quote: "they appear graphically equal and the criteria from 1A and 1B have been met. However, convergence must be verified graphically. Figure 5 shows a plot of the convergence from the table above. Note that the curve has not visually flattened out and that there is still a 21% error between the final average value of 124,099PSI and the previous hand calculations of 156,849PSI. Note that this method of meshing and iteration resulted in no mesh quality errors or warnings and met our main accuracy criteria, yet an error still exists in the model. This method of meshing was performed to illustrate a point. Often in a solid mesh there can exist very poorly shaped elements just below the surface although the number of elements along the surface appear adequate to ensure an accurate solution"

https://support.ansys.com/staticassets/ANSYS/stati...