In my last post, I solved for coil bind at full shock compression. It was an interesting exploration of that limit, but helpful replies by Greg and Brian pointed out the trike would be terminally undersprung at high accel/decel, so I am returning to the more traditional approach of solving for spring rate setting available wheel bump load to equal expected peak load under braking (front) and acceleration (rear).
Per my last post, I am seeking to minimize spring rate without riding on the bumpstops. To do so, remaining wheel bump load available at laden shock travel must be greater than expected peak compression load.
I would greatly appreciate any review of the following. Excel attached.
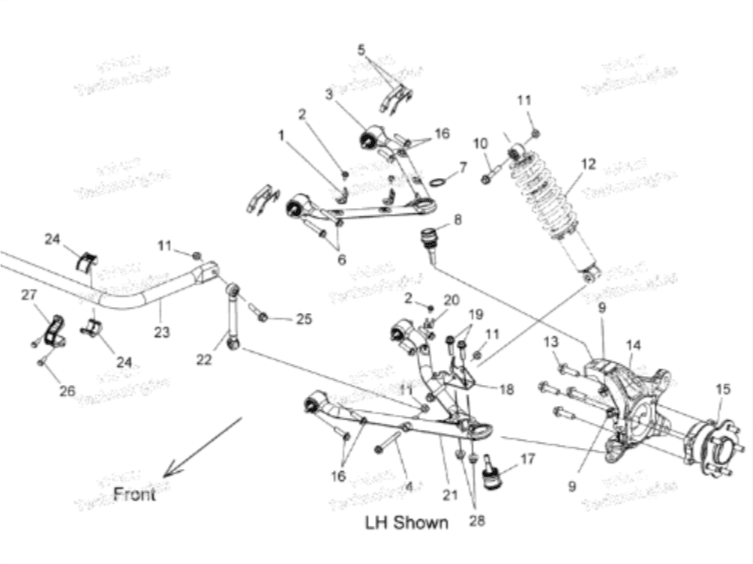
Load Estimates
Brake: 1950lbm laden weight * 1g braking decel = 1950lb, divide by 2 front wheels = 975lb per wheel
Accelerate: 0-60mph in 5.5sec. (2.7g per second of 0-60) divide by 5.5sec = 0.5g * 1950lbm = 970lb on single rear wheel
Cornering at 1.02g???
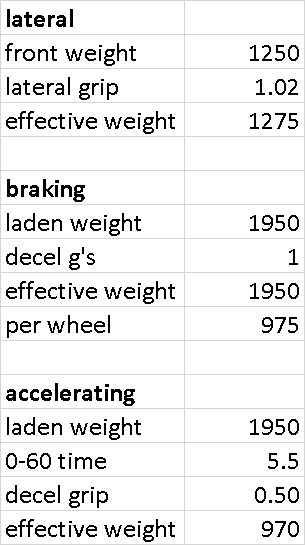
Shock Sizing
Current unladen ground clearance is 6"; target unladen clearance is 5" = body should lower 1".
To find motion ratio, divide lower A-arm pivot to shock mount (13.5") by pivot to balljoint (16") = 0.84. 1" lower @ wheel = 0.84" shorter shock.
Current shock compresses to 15.5" unladen, subtract 0.84" to find new unladen shock length of 14.7".
New shock collapses to 11", stroke of 4.87" extends to 15.87". Compressed to 14.7" unladen is 75% compression travel (3.7"), 25% extension travel (1.21").
Unladen Weight
Total weight unladen 1740lbm; corner weight unladen 570lbm minus 60lbm wheel & suspension = 505lbm sprung.
Spring angle of 54deg. Find spring angle adjustment factor by SIN(54deg in rad); multiply by shock motion ratio of 0.84 = corrected spring motion ratio of 0.68.
Sprung weight of 505lbm at wheel divided by 0.68 = 740lb at the spring.
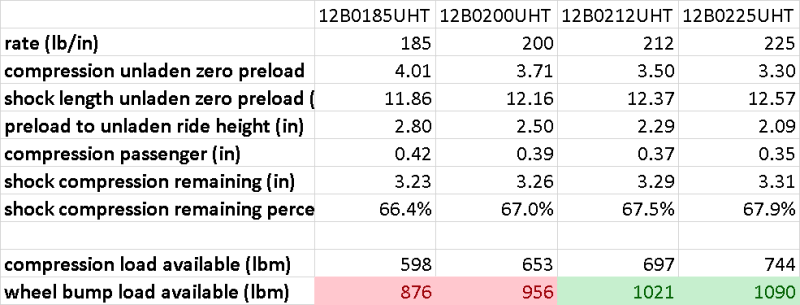
740lb divided by 212lb/in spring = 3.5" compression at zero preload. 15.87" extended shock compresses to 12.4".
Target unladen shock extension is 14.7", subtract 12.4" = 2.3" preload to extend shock to target ride height.
Laden Weight
Front corner weight when laden = 625lbm, subtract unladen corner weight of 570lbm = 55lbm of added passenger weight, divide by spring motion ratio of 0.68 = 78lb at the spring, divide by 212lb/in = 0.37" compression.
Unladen shock compression travel of 3.7" minus 0.37" = 3.3" (67.5%, nice!) remaining shock compression travel when laden.
3.3" remaining shock compression travel * 212lb/in = 697lb at the spring, divide by spring motion ratio of 0.68 = 1020lb available bump load at the wheel
1020lb available at the wheel > 970lb expected when braking at 1g
Per my last post, I am seeking to minimize spring rate without riding on the bumpstops. To do so, remaining wheel bump load available at laden shock travel must be greater than expected peak compression load.
I would greatly appreciate any review of the following. Excel attached.
Load Estimates
Brake: 1950lbm laden weight * 1g braking decel = 1950lb, divide by 2 front wheels = 975lb per wheel
Accelerate: 0-60mph in 5.5sec. (2.7g per second of 0-60) divide by 5.5sec = 0.5g * 1950lbm = 970lb on single rear wheel
Cornering at 1.02g???

Shock Sizing
Current unladen ground clearance is 6"; target unladen clearance is 5" = body should lower 1".
To find motion ratio, divide lower A-arm pivot to shock mount (13.5") by pivot to balljoint (16") = 0.84. 1" lower @ wheel = 0.84" shorter shock.
Current shock compresses to 15.5" unladen, subtract 0.84" to find new unladen shock length of 14.7".
New shock collapses to 11", stroke of 4.87" extends to 15.87". Compressed to 14.7" unladen is 75% compression travel (3.7"), 25% extension travel (1.21").

Unladen Weight
Total weight unladen 1740lbm; corner weight unladen 570lbm minus 60lbm wheel & suspension = 505lbm sprung.
Spring angle of 54deg. Find spring angle adjustment factor by SIN(54deg in rad); multiply by shock motion ratio of 0.84 = corrected spring motion ratio of 0.68.
Sprung weight of 505lbm at wheel divided by 0.68 = 740lb at the spring.
740lb divided by 212lb/in spring = 3.5" compression at zero preload. 15.87" extended shock compresses to 12.4".
Target unladen shock extension is 14.7", subtract 12.4" = 2.3" preload to extend shock to target ride height.
Laden Weight
Front corner weight when laden = 625lbm, subtract unladen corner weight of 570lbm = 55lbm of added passenger weight, divide by spring motion ratio of 0.68 = 78lb at the spring, divide by 212lb/in = 0.37" compression.
Unladen shock compression travel of 3.7" minus 0.37" = 3.3" (67.5%, nice!) remaining shock compression travel when laden.
3.3" remaining shock compression travel * 212lb/in = 697lb at the spring, divide by spring motion ratio of 0.68 = 1020lb available bump load at the wheel
1020lb available at the wheel > 970lb expected when braking at 1g


![[smile] [smile] [smile]](/data/assets/smilies/smile.gif)