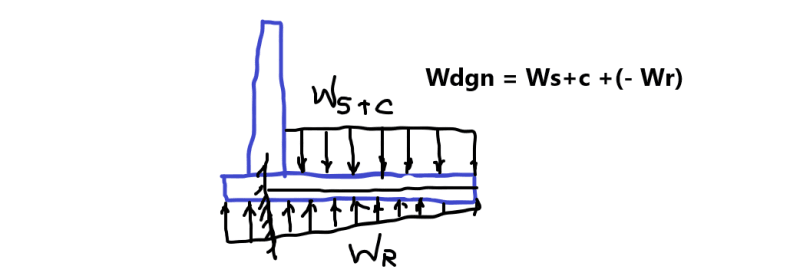
I am confused regarding the forced to be applied while designing the Heel in Retaining Wall.
Some books don't use the uplift force and use the only force F = Weight of Soil above Heel + Heel concrete weight.
and some book use the uplift force F = Weight of Soil above Heel + Heel concrete weight - force of Soil.
Which one designing Engineers use.
With the second one, the rebars will be reduced.
Some books don't use the uplift force and use the only force F = Weight of Soil above Heel + Heel concrete weight.
and some book use the uplift force F = Weight of Soil above Heel + Heel concrete weight - force of Soil.
Which one designing Engineers use.
With the second one, the rebars will be reduced.