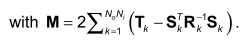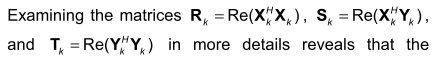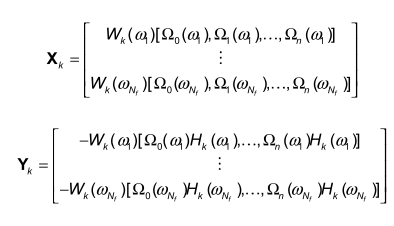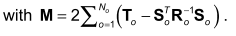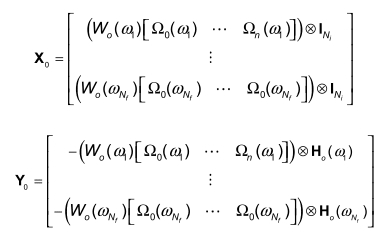Hello Everyone,
When using the poly-reference least squares complex frequency domain estimator (p-LSCF) to estimate modal parameters, you iteratively increase the model order and plot successive pole estimates on a stability diagram. In the literature it says you can only increase the model order in steps of Ni (number of inputs). Does anyone know why that is true?
For example:
RMFD - Right Matrix Fraction Description.

Is there a better place to post this question?
Regards,
When using the poly-reference least squares complex frequency domain estimator (p-LSCF) to estimate modal parameters, you iteratively increase the model order and plot successive pole estimates on a stability diagram. In the literature it says you can only increase the model order in steps of Ni (number of inputs). Does anyone know why that is true?
For example:
RMFD - Right Matrix Fraction Description.

Is there a better place to post this question?
Regards,