This question is mostly for the Math Smiths. We will be using one of our servo amplifiers to micro step a two phase stepper motor. The customers controller creates sine and cosine current commands, we supply two current loops.
The amplifier is a linear amplifier so the customers sensors don't get corrupted by PWM switching noise and as always, one wants to minimize power dissipation in the amplifier.
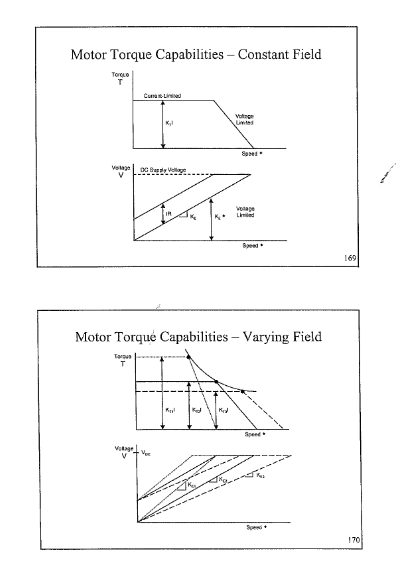
One can use maximum phase current up to the speed where you run out of B+ voltage to over come the motor BEMF and the voltage required to drive current into the phase inductance. Above that speed you can still accelerate but with reduced current.
So one needs to keep the voltage requirement constant as the speed increases but as the current goes down the acceleration decreases and so does the rate of change of velocity.
I see this as "The Rocket Velocity Problem" where the thrust decreases as the rocket velocity increases but at the same time the mass of the rocket decreases as the fuel is burned. So I can state the problem but have lost the math skills to solve the problem let alone even come up with the equation for velocity vs. time.
The amplifier is a linear amplifier so the customers sensors don't get corrupted by PWM switching noise and as always, one wants to minimize power dissipation in the amplifier.
One can use maximum phase current up to the speed where you run out of B+ voltage to over come the motor BEMF and the voltage required to drive current into the phase inductance. Above that speed you can still accelerate but with reduced current.
So one needs to keep the voltage requirement constant as the speed increases but as the current goes down the acceleration decreases and so does the rate of change of velocity.
I see this as "The Rocket Velocity Problem" where the thrust decreases as the rocket velocity increases but at the same time the mass of the rocket decreases as the fuel is burned. So I can state the problem but have lost the math skills to solve the problem let alone even come up with the equation for velocity vs. time.