-
1
- #1
ghost_rider
Mechanical
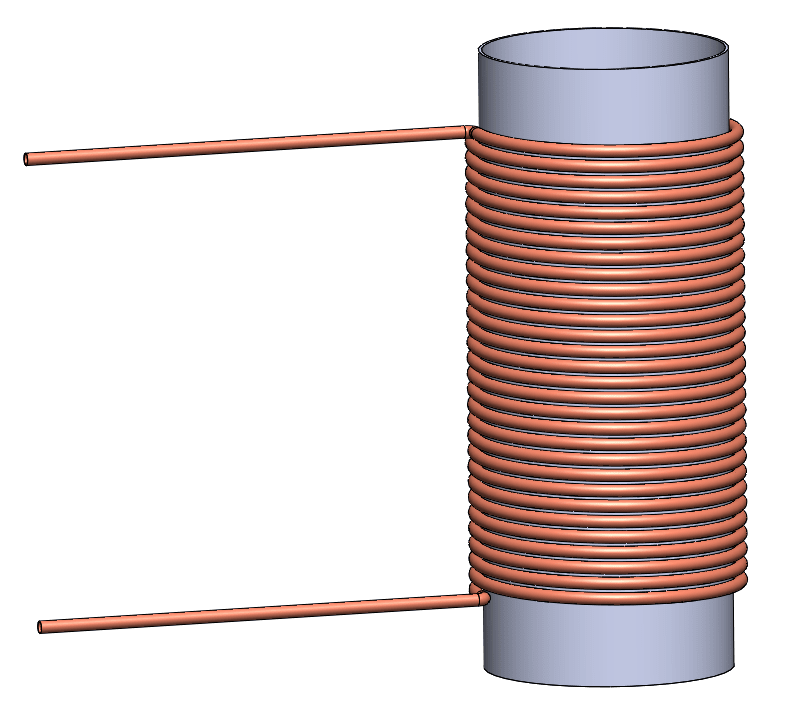
I have a copper coil wrapped around a stainless steel cylinder (please see attached). The temp. of inner surface of the cylinder is assumed to be 500C. Water will flow through the copper coil, entering at 20C and leaving at 60C (therefore the average water temp is 40C).
Now for the heat transfer from the coil wall to the water inside, Q=U A dT (W) can be used? I'm having difficulty in calculating U. Here, the area is the surface area of the coil. But, should dT be the difference between coil wall temp and avg. water temp? Before that, can I use same equation to determine heat transfer between cylinder and coil outer surface? Again, I'm having difficulty in U calc.
Once I have Q, I can use it to calculate the water flow rate required to achieve a gradient of 40C (60C-20C) for Q=m(mass flowrate) Cp dT (W)
It will be really helpful if anyone can please advice on U calculation. Also, on the method I have used to get flow rate.
Note: fuel is burnt inside the cylinder. However, to simplify the problem I am assuming the inside wall temp will be 500C.
Now for the heat transfer from the coil wall to the water inside, Q=U A dT (W) can be used? I'm having difficulty in calculating U. Here, the area is the surface area of the coil. But, should dT be the difference between coil wall temp and avg. water temp? Before that, can I use same equation to determine heat transfer between cylinder and coil outer surface? Again, I'm having difficulty in U calc.
Once I have Q, I can use it to calculate the water flow rate required to achieve a gradient of 40C (60C-20C) for Q=m(mass flowrate) Cp dT (W)
It will be really helpful if anyone can please advice on U calculation. Also, on the method I have used to get flow rate.
Note: fuel is burnt inside the cylinder. However, to simplify the problem I am assuming the inside wall temp will be 500C.