tlewis3348
Mechanical
I'm trying to find the formula for calculating the tensile stress area of a bolt. According to page 1528 of The Machinery's Handbook (29th Ed.), that formula is given as A_S=(π/4)*((d_m+d_p)/2)^2 where the pitch diameter is d_p=d−0.649519×P, and the minor diameter is d_m=d−1.299038×P.
I was trying to understand where the definitions of d_p and d_m come from. The Wikipedia page for the Unified Thread Standard ( was very helpful for understanding that. However, it is not clear where the equation for d_m comes from. The value 1.299038 is equivalent to 3*sqrt(3)/4. Translating this to be in terms of H instead of P results in d_m=d−2*(3/4)*H. In other words, it would appear that the boxed dimension in the drawing below (versions of which appear on pages 1807, 1912, and 1973 of the handbook mentioned above) should be .75*H instead of .625*H.
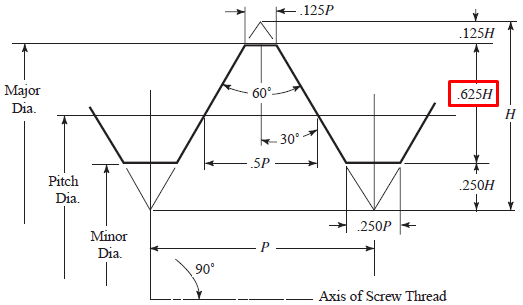
I'm assuming I must be missing something obvious here because I'm seeing variations of the formula for A_S listed above everywhere. The best I can figure is that the equation for A_S assumes that the outermost 1/8th of the thread's V is included in the nominal diameter of the bolt. However, I can't find any justification for this. If someone could explain it to me, I would greatly appreciate it.
I was trying to understand where the definitions of d_p and d_m come from. The Wikipedia page for the Unified Thread Standard ( was very helpful for understanding that. However, it is not clear where the equation for d_m comes from. The value 1.299038 is equivalent to 3*sqrt(3)/4. Translating this to be in terms of H instead of P results in d_m=d−2*(3/4)*H. In other words, it would appear that the boxed dimension in the drawing below (versions of which appear on pages 1807, 1912, and 1973 of the handbook mentioned above) should be .75*H instead of .625*H.

I'm assuming I must be missing something obvious here because I'm seeing variations of the formula for A_S listed above everywhere. The best I can figure is that the equation for A_S assumes that the outermost 1/8th of the thread's V is included in the nominal diameter of the bolt. However, I can't find any justification for this. If someone could explain it to me, I would greatly appreciate it.
