Hello,
I am trying to calculate the state of steam between the nozzle and impulse turbine wheel for tip and labyrinth leakage purposes for a specific steam loss model, and having some troubles with it.
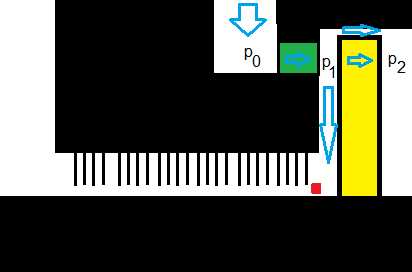
Using _0 before nozzle, _1 after nozzle but before turbine blades, and _2 after turbine blades. I have the following information from process (simplified):
p0 = 1600 kPa
p2 = 500 kPa
T0 = 350 C
T2 = 250 C
Calculated/figured the following values:
h0 = 3147 kJ/kg
h2 = 2961 kJ/kg
Δh = 186 kJ/kg
v0 = 60 m/s
v1 = SQRT(2000*Δh+v02) = 612 m/s
Assumed nozzle speed ratio v1/v1,is = 0.95
In isentropic case (ratio is 1):
Δhis = 186/0.952 = 206 kJ/kg, so nozzle loss therefore is:
hn = Δhis-Δh = 20 kJ/kg (and v1,is = 644 m/s)
But my major question is, how do I combine all this information? I don't know the isentropic efficiency for turbine wheel (without nozzle) either. I was going to solve it after knowing (p1,T1), since I can calculate the isentropic efficiency for nozzle+wheel combination using p0,T0 to p2,T2 (which is 0.65, fairly common for Curtis wheel). Seems I am missing some theory behind this. Can someone shed some light on how to proceed with this? Nozzle loss should be loss in flow energy (644 -> 612), increase in temperature and loss in entropy as far as I know.
I tried to calculate h1=h0-hn and combine that with p1=p2. What actually happens with the temperature T1 in relation to T0 or T2?
How can I account velocity in (p,T,h,S)-table? I have a software to calculate Curtis wheel's isentropic efficiency using (pin,Tin,is%,pout) so I can't account velocity in as input variable? If I use p2 as p, I get 0 W power obviously.
And is the energy transfer in wheel 186 kJ/kg * nwheel,is% or (186-20)=166 kJ/kg * nwheel,is%? is% = isentropic efficiency in wheel
If p0 > p1 > p2, how can I calculate it? Can I assume incompressible flow and use Bernoulli equation p1 = p0 + 1/2 ρv02 - 1/2 ρv12 (assume ρ=ρ0=ρ1 with enough accuracy) and look for T1 through h1=h0-hn?
I am trying to calculate the state of steam between the nozzle and impulse turbine wheel for tip and labyrinth leakage purposes for a specific steam loss model, and having some troubles with it.
Using _0 before nozzle, _1 after nozzle but before turbine blades, and _2 after turbine blades. I have the following information from process (simplified):
p0 = 1600 kPa
p2 = 500 kPa
T0 = 350 C
T2 = 250 C
Calculated/figured the following values:
h0 = 3147 kJ/kg
h2 = 2961 kJ/kg
Δh = 186 kJ/kg
v0 = 60 m/s
v1 = SQRT(2000*Δh+v02) = 612 m/s
Assumed nozzle speed ratio v1/v1,is = 0.95
In isentropic case (ratio is 1):
Δhis = 186/0.952 = 206 kJ/kg, so nozzle loss therefore is:
hn = Δhis-Δh = 20 kJ/kg (and v1,is = 644 m/s)
But my major question is, how do I combine all this information? I don't know the isentropic efficiency for turbine wheel (without nozzle) either. I was going to solve it after knowing (p1,T1), since I can calculate the isentropic efficiency for nozzle+wheel combination using p0,T0 to p2,T2 (which is 0.65, fairly common for Curtis wheel). Seems I am missing some theory behind this. Can someone shed some light on how to proceed with this? Nozzle loss should be loss in flow energy (644 -> 612), increase in temperature and loss in entropy as far as I know.
I tried to calculate h1=h0-hn and combine that with p1=p2. What actually happens with the temperature T1 in relation to T0 or T2?
How can I account velocity in (p,T,h,S)-table? I have a software to calculate Curtis wheel's isentropic efficiency using (pin,Tin,is%,pout) so I can't account velocity in as input variable? If I use p2 as p, I get 0 W power obviously.
And is the energy transfer in wheel 186 kJ/kg * nwheel,is% or (186-20)=166 kJ/kg * nwheel,is%? is% = isentropic efficiency in wheel
If p0 > p1 > p2, how can I calculate it? Can I assume incompressible flow and use Bernoulli equation p1 = p0 + 1/2 ρv02 - 1/2 ρv12 (assume ρ=ρ0=ρ1 with enough accuracy) and look for T1 through h1=h0-hn?