Mario_Aero92
Aerospace
Hi!
I have the following system:
x is am imposed motion and y is the output that I obtain.
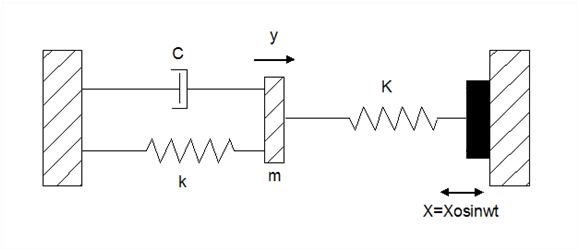
I would like to calculate the natural frequency of the system. My intuition says that it is equal to sqrt((K+k)/m), but I am not sure how to derive this value from the equation of motion of the system.
Could you help me with this?
Thank you in advance!
I have the following system:
x is am imposed motion and y is the output that I obtain.

I would like to calculate the natural frequency of the system. My intuition says that it is equal to sqrt((K+k)/m), but I am not sure how to derive this value from the equation of motion of the system.
Could you help me with this?
Thank you in advance!
