teknomania
Mechanical
Hello,
During my tasks in different disciplines, I am reaching some new performance measure as according to the topic studied. I already used multi-regression in some and, if that was not enough to fit my data, I used interpolation method 'The Vandermonde Method' and lately discovered the powerful griddata function by Matlab.
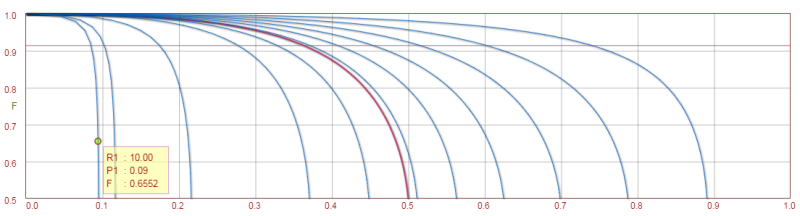
I need to derive new expression/equations for the data I reach each time (like regression coefficients so that I can use them in my model). My question arises since I have no idea how the old scientists could find the advanced expressions for their data (Please check the formulations below). For example, how one could put the relation for the correction factor as a function of R and P as given below. As you can see, the relations of R and P with correction factor is not straightforward to be understood. Normally the curve of correction factor seems to be power-like regression for each P with changing R values. But the formulation below is totally out-of-world.
I believe that there is a topic in mathematics like regression, interpolation etc. for such expression deriving. Checked google but couldn't find anything. Any help, guidance can be rewarding.
In Example:
Nusselt correlations
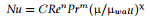
or
Correction Factor - LMTD Theory(most inspiring one)
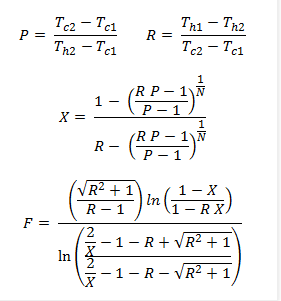
“In life, the truest guide is science” – Mustafa Kemal Atatürk
During my tasks in different disciplines, I am reaching some new performance measure as according to the topic studied. I already used multi-regression in some and, if that was not enough to fit my data, I used interpolation method 'The Vandermonde Method' and lately discovered the powerful griddata function by Matlab.
I need to derive new expression/equations for the data I reach each time (like regression coefficients so that I can use them in my model). My question arises since I have no idea how the old scientists could find the advanced expressions for their data (Please check the formulations below). For example, how one could put the relation for the correction factor as a function of R and P as given below. As you can see, the relations of R and P with correction factor is not straightforward to be understood. Normally the curve of correction factor seems to be power-like regression for each P with changing R values. But the formulation below is totally out-of-world.
I believe that there is a topic in mathematics like regression, interpolation etc. for such expression deriving. Checked google but couldn't find anything. Any help, guidance can be rewarding.
In Example:
Nusselt correlations
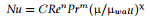
or
Correction Factor - LMTD Theory(most inspiring one)
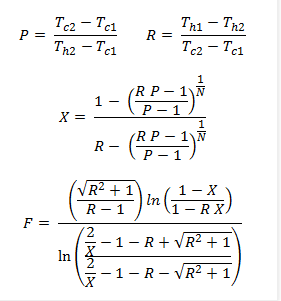
“In life, the truest guide is science” – Mustafa Kemal Atatürk