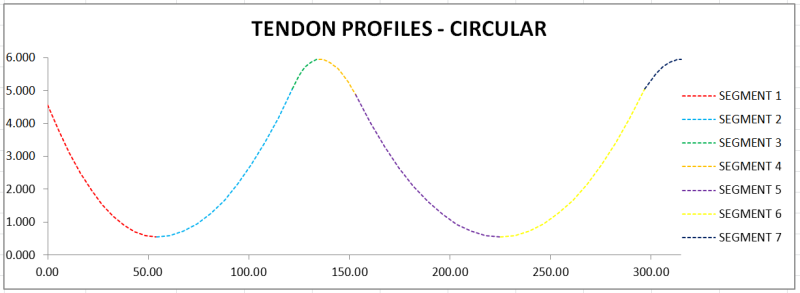
Hi all!
I've searched far and wide but haven't been able to find this information: how does one calculate the slopes of PT cable knowing the locations of the inverts?
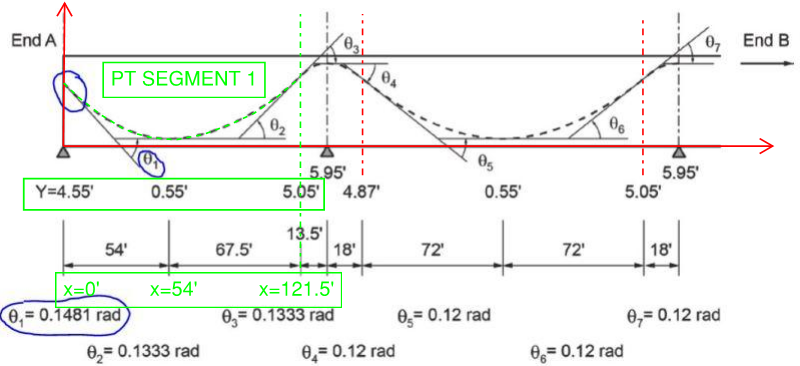
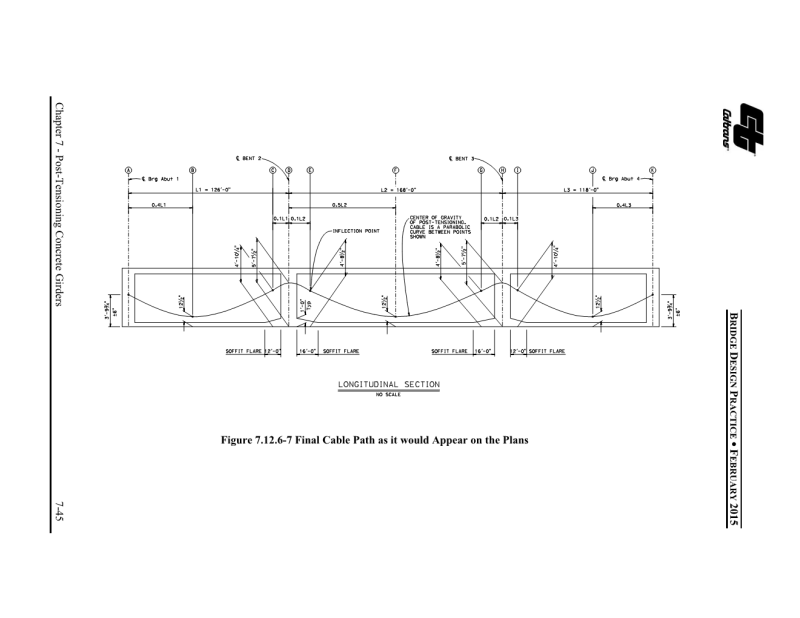
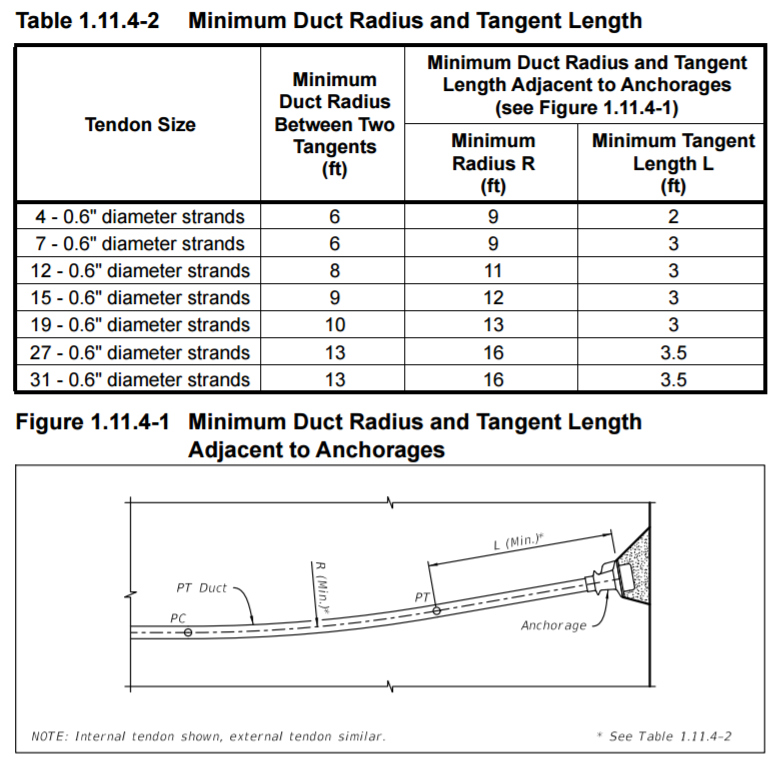
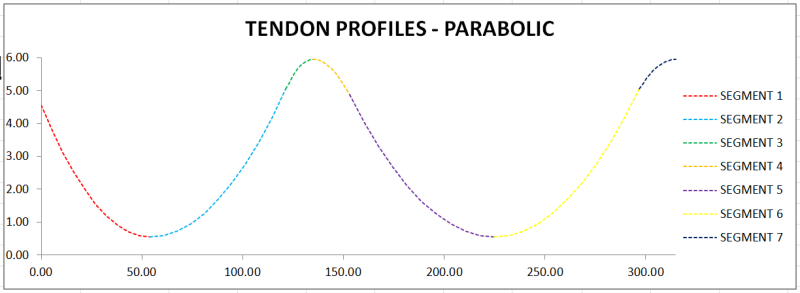
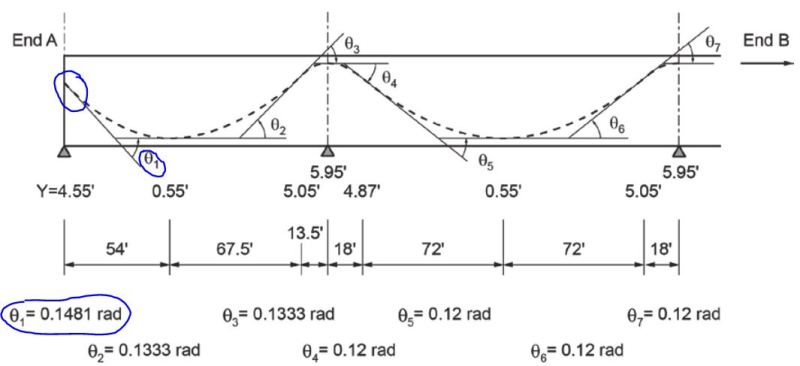
The below is an example from a US DoT guide. It shows that they have found the values of theta, but they have not shown how.
I've looked at using equations for catenaries, but they require knowing the tension and/or weight of the cable which in this case is completely irrelevant as in the field, the cable (or rather, duct) will be supported by whatever means required to achieve the needed drape. Without this information it seems one is required to solve equations with imaginary numbers and inverse hyperbolic equations with multiple unknowns (ain't nobody got time for that).
I know there is software which solves this (e.g. RAPT). However, I want to implement this in excel or Mathcad and hence would be happy with a reasonably accurate approximation.
No references I've seen on PT design seem to cover this point. Is this just common knowledge like a²+b²=c² and I have just neglected to pick it up throughout my education and career?
Any ideas would be greatly appreciated.
I've searched far and wide but haven't been able to find this information: how does one calculate the slopes of PT cable knowing the locations of the inverts?
The below is an example from a US DoT guide. It shows that they have found the values of theta, but they have not shown how.

I've looked at using equations for catenaries, but they require knowing the tension and/or weight of the cable which in this case is completely irrelevant as in the field, the cable (or rather, duct) will be supported by whatever means required to achieve the needed drape. Without this information it seems one is required to solve equations with imaginary numbers and inverse hyperbolic equations with multiple unknowns (ain't nobody got time for that).
I know there is software which solves this (e.g. RAPT). However, I want to implement this in excel or Mathcad and hence would be happy with a reasonably accurate approximation.
No references I've seen on PT design seem to cover this point. Is this just common knowledge like a²+b²=c² and I have just neglected to pick it up throughout my education and career?
Any ideas would be greatly appreciated.