Draining a Pipeline System

Question

Draining a Pipeline System

Steve_o (Civil/Environmental)

(OP)

28 Oct 16 15:10

So, I have this problem. There are 3 Scenarios. All 3 scenarios have the same geometric layout:

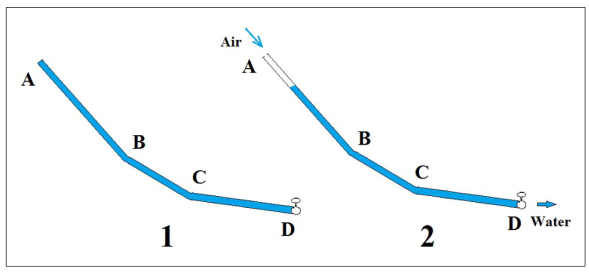
The user can choose the elevations and pipe diameters and roughness's to drain the pipe out the pipe with or without an air valve at A.

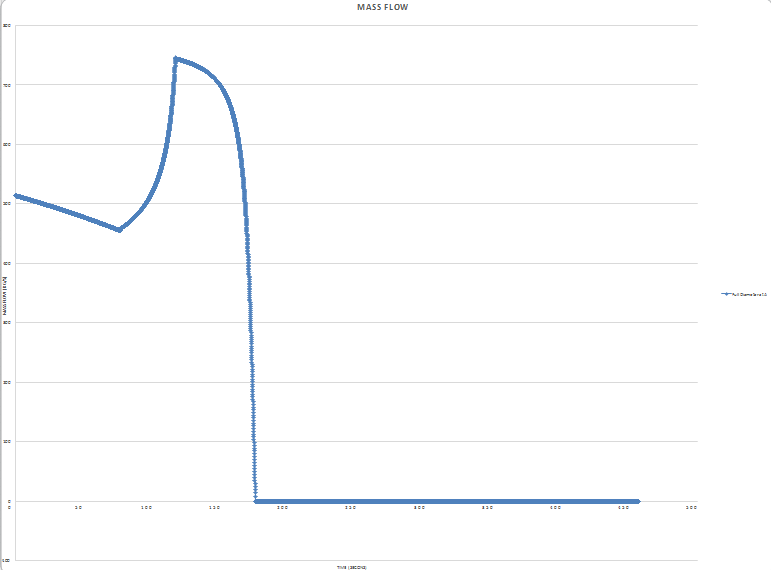
I want to know why (using Bernoulli) if I make the pipe diameter smaller between the nodes B and C the Q versus time does this (time x-axis):

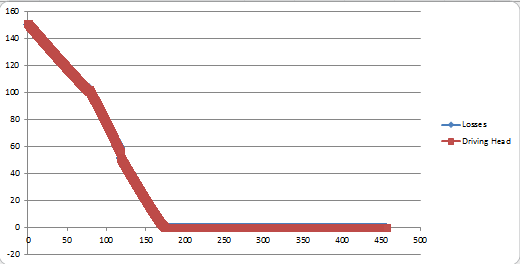
This happens while the total head of the system does this (time x-axis):

I have checked, re-checked and re-checked my maths and my Bernoulli assumptions several times and my colleagues got the same answer. Any ideas if this is correct or not?

This occurred whether there was an air valve or not.

Drew08 (Civil/Environmental) · Answer 1 · 2016-10-31 13:00:00

Actually makes sense to me. With all sections equal in diameter, the system drains only as fast as gravity can pull the water out. Energy loss through any section is proportional to its length. However, when the middle section is smaller in diameter, water is being pulled through it faster than gravity can push it making its share of energy loss greater than its length relative to the other sections. As water drains from the smaller pipe (effectively decreasing its length, the efficiency of the system as a whole increases faster than the total system head decreases resulting in an increasing flow rate as water drains from the smaller pipe.

Another way to put it, water can't drain out of the last pipe faster than water can get into it, but once the smaller middle pipe is fully drained, there is no such restriction.

All of this of course assumes the last pipe has full flow. If there is a significant restriction caused by the middle pipe, the last pipe might not achieve full flow.

Come Join Us!

Posting Guidelines

Related Projects

Jobs

Draining a Pipeline System