Consider a 138kv system with 4" bus for each phase (attached example). In which direction do the SC forces on each bus act? I am trying to figure out if any SC forces will make their way to the foundation or if they cancel out at the beam. Talking to one engineer, he mentioned that the SC forces will cancel out at the beam level for being equal and opposite. But I think that the foundation should be designed for a horizontal force from at least one bus.
Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations MintJulep on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Short circuit force direction 3
- Thread starter WWTEng
- Start date
- Status
- Not open for further replies.
- Moderator
- #2
The direction, consider two physically parallel conductors.
If the current is in the same direction the conductors will pull together. (Conductors in parallel electrically.)
If the current is in the opposite direction the conductors will push apart. (Conductors for a circuit, such as "A" phase and "B" phase.)
If the support insulators are mounted on a rigid beam there will be no net force transmitted to the foundation.
However, step back and look at the complete installation. There may be interaction with parallel circuits which may produce a force on the foundation.
Bill
--------------------
"Why not the best?"
Jimmy Carter
If the current is in the same direction the conductors will pull together. (Conductors in parallel electrically.)
If the current is in the opposite direction the conductors will push apart. (Conductors for a circuit, such as "A" phase and "B" phase.)
If the support insulators are mounted on a rigid beam there will be no net force transmitted to the foundation.
However, step back and look at the complete installation. There may be interaction with parallel circuits which may produce a force on the foundation.
Bill
--------------------
"Why not the best?"
Jimmy Carter
- Thread starter
- #3
-
1
- Moderator
- #4
The current in each bus will create a magnetic field surrounding each bus.
The fields interact with each other.
The instantaneous current in each bus bar is 1/3 cycle ahead or behind the current in the other two bus bars.
The force on the center bus bar will alternate to one side or the other.
The forces in a flat bus bar arrangement will be either towards or apart from each other.
For a trefoil arrangement it gets more complicated.
Bill
--------------------
"Why not the best?"
Jimmy Carter
The fields interact with each other.
The instantaneous current in each bus bar is 1/3 cycle ahead or behind the current in the other two bus bars.
The force on the center bus bar will alternate to one side or the other.
The forces in a flat bus bar arrangement will be either towards or apart from each other.
For a trefoil arrangement it gets more complicated.
Bill
--------------------
"Why not the best?"
Jimmy Carter
-
2
- #5
The IEEE Std. 605-1998. IEEE Guide for Design of Substation Rigid-Bus Structures provides a good guidance to determine the forces on busses. The
1) SC forces: . Fsc= 3.6*Γ(Isc)2/107.D
Where:
Fsc = Force per unit length (lbf/ft)
Isc = Symmetrical RMS fault current (A)
D = Rigid bus center-to-center (ft)
Γ = Constant based on type of fault (See table below)
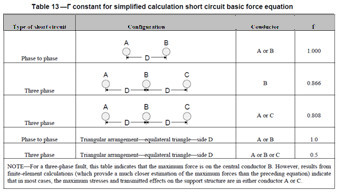
For the max. forces, see the note on the table enclosed
2) Videos for SC on rigid bus:
i) ii)
1) SC forces: . Fsc= 3.6*Γ(Isc)2/107.D
Where:
Fsc = Force per unit length (lbf/ft)
Isc = Symmetrical RMS fault current (A)
D = Rigid bus center-to-center (ft)
Γ = Constant based on type of fault (See table below)

For the max. forces, see the note on the table enclosed
2) Videos for SC on rigid bus:
i) ii)
- Thread starter
- #6
davidbeach
Electrical
Modern standards, at least in the IEEE/ANSI world, are based on symmetrical at some stated X/R; thus the asymmetrical case is covered. If the stated X/R is exceeded there will be adjustment factors; again addressing the asymmetrical case within the symmetrical ratings.
- Moderator
- #8
This may depend on the meaning of design.
If design means selecting a tested and approved assembly or device that has been rated to withstand a given fault current then davidbeach's answer is correct.
Most designs are based on symmetrical ratings.
These are the ratings that most of us use from day to day.
The concept of Available Short Circuit Current is related to this.
The ASCC is easy to calculate from the rated current and the % impedance voltage. Use that value to select appropriately rated equipment and you have a safe and compliant installation.
However, if design is taken to mean the original design of an assembly or device to withstand the forces associated with fault currents then the maximum asymmetrical current must be considered.
Magnetic forces are proportional to the square of the current. The peak asymmetrical current must be used to calculate the maximum force.
The actual fault current is generally greater than the ASCC and the interrupting and/or withstand capability of the devices is greater than the symmetrical current as indicated by the ASCC.
However the issues of maximum forces and asymmetrical or offset currents are addressed in the background and most of us never need to concern ourselves with them.
It is a happy coincidence if the fault current does not exceed the Available Short Circuit Current. In most instances the fault current will be asymmetrical and the peak current will be greater than that calculated from the ASCC.
The maximum force due to an offset or fully asymmetrical current may approach 2.82 times the force of an RMS symmetrical current or the ASCC.
A word of explanation, this is not apples and apples. The magnetic forces are maximum at the peak of the current. The ratio between RMS and average is √2, so although the ratio between symmetrical RMS and peak asymmetrical is 2.8:1 (2 x √2) the ratio between the peak currents is 2:1 and the ratio between the maximum magnetic forces is 4:1 not 8:1 as a ratio of 2.8:1 may suggest.
Many engineers may spend their careers correctly sizing equipment for commercial and industrial installations and never encounter an application with an X:R ratio greater than the ratio at which the equipment is certified.
A rare exception to the excellent explanation given by davidbeach:
Years ago I worked on a 500kV capacitor station. We had long IPS bus runs supported on 500kV insulators which were in turn individually mounted on concrete pillars. The design engineer would have had to design the supports to withstand the maximum forces that may be encountered with an asymmetrical fault current.
Bill
--------------------
"Why not the best?"
Jimmy Carter
If design means selecting a tested and approved assembly or device that has been rated to withstand a given fault current then davidbeach's answer is correct.
Most designs are based on symmetrical ratings.
These are the ratings that most of us use from day to day.
The concept of Available Short Circuit Current is related to this.
The ASCC is easy to calculate from the rated current and the % impedance voltage. Use that value to select appropriately rated equipment and you have a safe and compliant installation.
However, if design is taken to mean the original design of an assembly or device to withstand the forces associated with fault currents then the maximum asymmetrical current must be considered.
Magnetic forces are proportional to the square of the current. The peak asymmetrical current must be used to calculate the maximum force.
The actual fault current is generally greater than the ASCC and the interrupting and/or withstand capability of the devices is greater than the symmetrical current as indicated by the ASCC.
However the issues of maximum forces and asymmetrical or offset currents are addressed in the background and most of us never need to concern ourselves with them.
It is a happy coincidence if the fault current does not exceed the Available Short Circuit Current. In most instances the fault current will be asymmetrical and the peak current will be greater than that calculated from the ASCC.
The maximum force due to an offset or fully asymmetrical current may approach 2.82 times the force of an RMS symmetrical current or the ASCC.
A word of explanation, this is not apples and apples. The magnetic forces are maximum at the peak of the current. The ratio between RMS and average is √2, so although the ratio between symmetrical RMS and peak asymmetrical is 2.8:1 (2 x √2) the ratio between the peak currents is 2:1 and the ratio between the maximum magnetic forces is 4:1 not 8:1 as a ratio of 2.8:1 may suggest.
Many engineers may spend their careers correctly sizing equipment for commercial and industrial installations and never encounter an application with an X:R ratio greater than the ratio at which the equipment is certified.
A rare exception to the excellent explanation given by davidbeach:
Years ago I worked on a 500kV capacitor station. We had long IPS bus runs supported on 500kV insulators which were in turn individually mounted on concrete pillars. The design engineer would have had to design the supports to withstand the maximum forces that may be encountered with an asymmetrical fault current.
Bill
--------------------
"Why not the best?"
Jimmy Carter
WWTEng said:...bus work as well as ground grid is designed for Symmetrical only.
To simplify calculations, many EE equations are based in simplified formulas with the symmetrical fault current affected by factors embedded in the equations to account for the asymmetrical current effect (ex X/R,√2, decrement factor, etc.).
For reference below are couple of remarks to consider:
a)Bus work: Calc. is based primarily in maximum peak force it is indirectly associated with the peak asymmetric SC current.
b)Ground Grid: IEEE Std 80 It is based on the energy content absorbed by the body. This is indirectly associated with the equivalent rms value of the asymmetrical current wave for the maximum time of possible shock exposure.
- Status
- Not open for further replies.
Similar threads
- Replies
- 4
- Views
- 1K
- Replies
- 1
- Views
- 2K
- Locked
- Question
- Replies
- 5
- Views
- 2K
- Locked
- Question
- Replies
- 10
- Views
- 2K
