-
9
- #1
I've put this together in response to a recent request for information on modelling a flexible hose (pictured in Thread 560-176891), so here's a step-by-step guide to the the method I used, but while I'm at it I'll elaborate a little...
There's no shortage of pictures so most of them appear as thumbnails, C L I C K on these to open them up in another window.
(1)
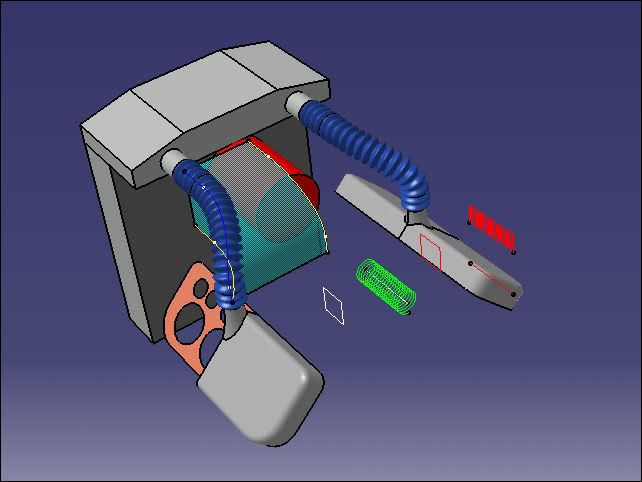
This simplistic model ([1) is suitable for modelling one of a pair of top radiator hoses using Law and Sweep tools, it's also is an opportunity to demonstrate the use of Combine Curve to construct the guide curve for the (left) hose. Let's assume that the path of the hose centreline is known in plan and side elevation (shown in yellow), as on a drawing, then using the Combine Curve tool in default Normal mode (2) the (blue) resultant curve is made. The two known planar curves are components of a space curve - the transparent ruled surfaces show how the solution is the intersection of two implicit surfaces. Of course, a similar result could have been achieved directly with a spline but the orthogonal component approach is worth mentioning.
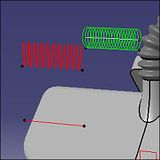
(2)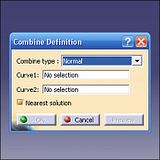 (3)
(3)  (4)
(4) 
To define the flexible hose corrugations a helix (green) is made along an axis line; the diameter of the helix will be the amplitude, or depth, of the corrugations, while the number of turns and the ratio of pitch to axis length are important, the axis length does not have to the same as the hose guide curve. This is because the Law will apply itself to the length of the object curve - whatever that may be. Nothing has to be spot-on first time as it can all be altered later.
In this example a helix is used because the law is going to be sinusoidal. The form of the corrugations can be whatever the user fancies - as at this stage we are actually drawing a graph of the corrugations. To get a graph from the 3D helix, it is normally projected onto a plane - somewhere out of the way (beside the right cylinder head will do), and a line positioned underneath the projected curve. The distance between them defines the overall diameter of the hose (3).
(5) (6)
(6)  (7)
(7) 
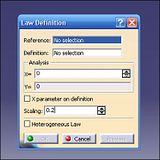
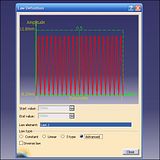
Open the Law tool (4): the Reference is the red line under the projected curve, and the Definition is the curve itself. The Scale is 0.2 only because I've made the law graph 5 times actual size so that I can see what I'm doing. The new Law has now appeared on the bottom of the Tree.
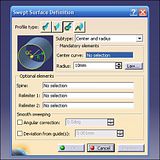
Now open the Sweep tool (5) and find the Centre and Radius option; select the Centre Curve, ignore the radius, and select Law. This action opens up another box: select the Advanced option and the click on the Law stored in the Specification tree (6). OK, and that's it, the corrugated surface is mapped onto the centre (guide) curve (7) .
---------------o0o---------------
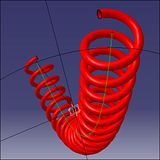
Another interesting Law-Sweep combination is when there is no obvious way way of constructing a particular curve. A curve that may be seen everyday - and not noticed; a simple, coiled air hose, like those between a truck and a semi-trailer (8).
How to model one in Catia V5 with the Helix Curve tool isn't immediately obvious (in R14 anyway), as the axis has to be linear. But, in Sweep, a helical surface can be wound along a curve, it's outer boundary saved, and the surface hidden.
(8) (9)
(9)  (10)
(10) 
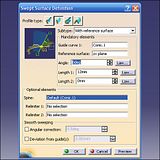
Open the Sweep tool and find the With Reference Surface option (9). There are two versions of this; one uses an existing profile (line or curve), while the second uses an implicit line, which is normal to the axis. You just enter the length of it. The guide curve, in this case, is the conic; the reference surface is something to start the angle of twist from.
Disregard the Angle and select Law, then select Linear. The Start value remains at 0, the End value (10) defines how many turns the helix will have - I'd start at 360 degrees and see if it's going to work (11) . Then edit the law to give the number of turns required. You don't have do any sums to find out how many degrees there are in so many turns - just enter "360*n" (number of turns) - it'll work it out (12).
In fact, any of it can be altered later - I tend to get something like this functioning first, and then fine tune it.
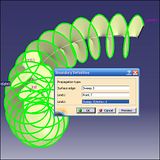
The implicit edge of the sweep can be used dirctly as a guide curve for the other sweep, but I prefer to use the Boundary - I think it's better practice...(13)
(11)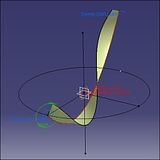 (12)
(12) 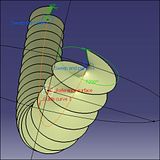 (13)
(13) 
In the last picture a black helical curve has been wound along a green parabolic conic, and a circular sectioned, corrugated surface formed on that (14) - a Case of Law on Law...
I doubt if the need to model hoses, etc is likely to happen very often; this is all about a modelling method and practice: these are a few of many examples of Laws controlling Surfaces.
(14)

There's no shortage of pictures so most of them appear as thumbnails, C L I C K on these to open them up in another window.
(1)

This simplistic model ([1) is suitable for modelling one of a pair of top radiator hoses using Law and Sweep tools, it's also is an opportunity to demonstrate the use of Combine Curve to construct the guide curve for the (left) hose. Let's assume that the path of the hose centreline is known in plan and side elevation (shown in yellow), as on a drawing, then using the Combine Curve tool in default Normal mode (2) the (blue) resultant curve is made. The two known planar curves are components of a space curve - the transparent ruled surfaces show how the solution is the intersection of two implicit surfaces. Of course, a similar result could have been achieved directly with a spline but the orthogonal component approach is worth mentioning.
(2)
 (3)
(3)  (4)
(4) 
To define the flexible hose corrugations a helix (green) is made along an axis line; the diameter of the helix will be the amplitude, or depth, of the corrugations, while the number of turns and the ratio of pitch to axis length are important, the axis length does not have to the same as the hose guide curve. This is because the Law will apply itself to the length of the object curve - whatever that may be. Nothing has to be spot-on first time as it can all be altered later.
In this example a helix is used because the law is going to be sinusoidal. The form of the corrugations can be whatever the user fancies - as at this stage we are actually drawing a graph of the corrugations. To get a graph from the 3D helix, it is normally projected onto a plane - somewhere out of the way (beside the right cylinder head will do), and a line positioned underneath the projected curve. The distance between them defines the overall diameter of the hose (3).
(5)
 (6)
(6)  (7)
(7) 
Open the Law tool (4): the Reference is the red line under the projected curve, and the Definition is the curve itself. The Scale is 0.2 only because I've made the law graph 5 times actual size so that I can see what I'm doing. The new Law has now appeared on the bottom of the Tree.
Now open the Sweep tool (5) and find the Centre and Radius option; select the Centre Curve, ignore the radius, and select Law. This action opens up another box: select the Advanced option and the click on the Law stored in the Specification tree (6). OK, and that's it, the corrugated surface is mapped onto the centre (guide) curve (7) .
---------------o0o---------------
Another interesting Law-Sweep combination is when there is no obvious way way of constructing a particular curve. A curve that may be seen everyday - and not noticed; a simple, coiled air hose, like those between a truck and a semi-trailer (8).
How to model one in Catia V5 with the Helix Curve tool isn't immediately obvious (in R14 anyway), as the axis has to be linear. But, in Sweep, a helical surface can be wound along a curve, it's outer boundary saved, and the surface hidden.
(8)
 (9)
(9)  (10)
(10) 
Open the Sweep tool and find the With Reference Surface option (9). There are two versions of this; one uses an existing profile (line or curve), while the second uses an implicit line, which is normal to the axis. You just enter the length of it. The guide curve, in this case, is the conic; the reference surface is something to start the angle of twist from.
Disregard the Angle and select Law, then select Linear. The Start value remains at 0, the End value (10) defines how many turns the helix will have - I'd start at 360 degrees and see if it's going to work (11) . Then edit the law to give the number of turns required. You don't have do any sums to find out how many degrees there are in so many turns - just enter "360*n" (number of turns) - it'll work it out (12).
In fact, any of it can be altered later - I tend to get something like this functioning first, and then fine tune it.
The implicit edge of the sweep can be used dirctly as a guide curve for the other sweep, but I prefer to use the Boundary - I think it's better practice...(13)
(11)
 (12)
(12)  (13)
(13) 
In the last picture a black helical curve has been wound along a green parabolic conic, and a circular sectioned, corrugated surface formed on that (14) - a Case of Law on Law...
I doubt if the need to model hoses, etc is likely to happen very often; this is all about a modelling method and practice: these are a few of many examples of Laws controlling Surfaces.
(14)

