nikoD
Mechanical
- Oct 5, 2020
- 6
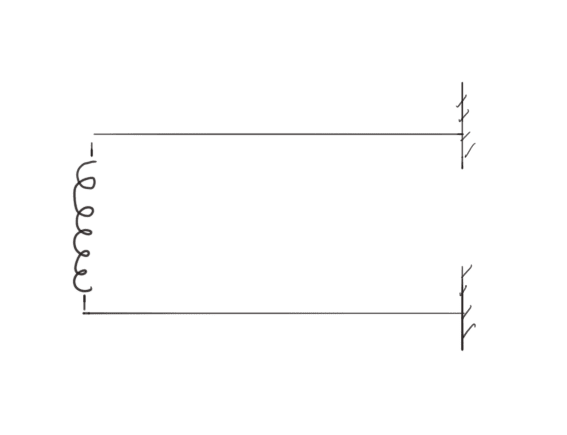
I have a friend who asked me how I would go about analyzing the max value of P in the situation shown in the picture.
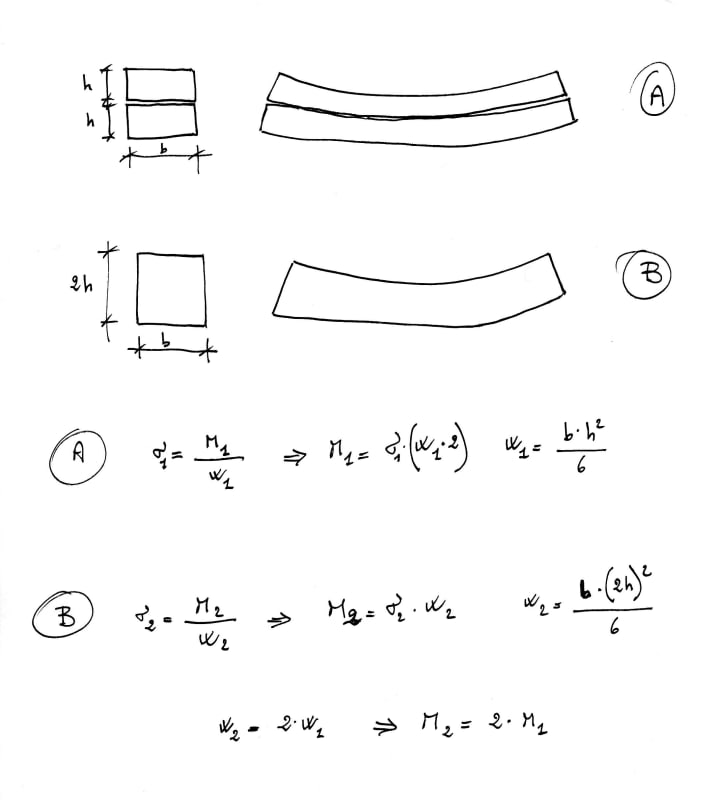
Two steel profiles are fitted into each other. Both are fixed to the support, but the beams are only connected to each other with spot welds at the beams' ends.
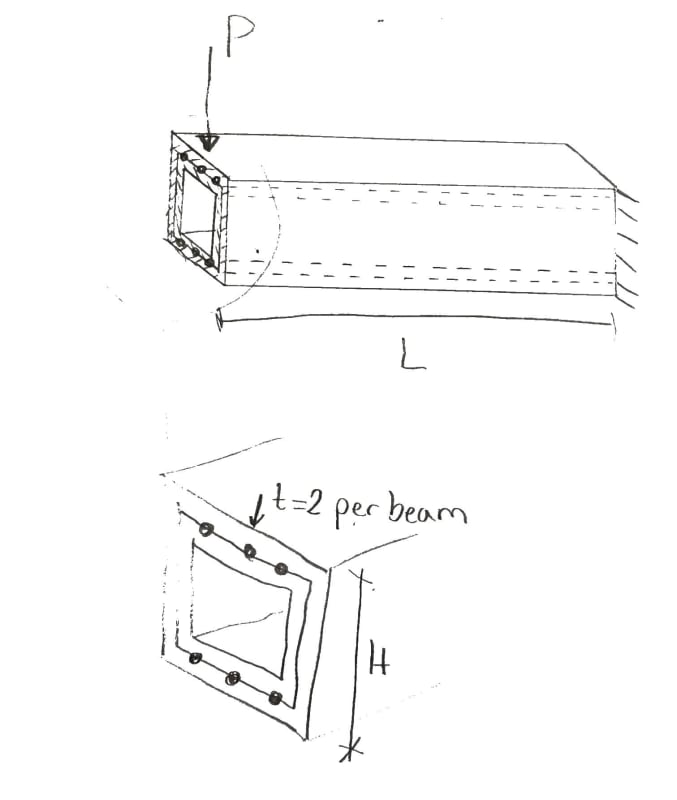
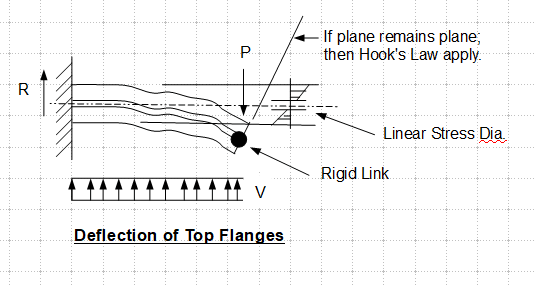
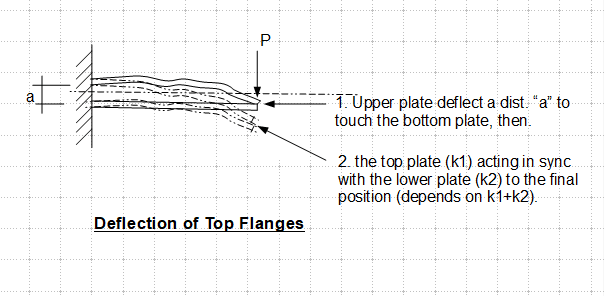
To me it looks as if the stresses from the outer profile must be transferred to the inner profile through the spot welds, which could reduce the load that the profiles can withstand.
[ul]
[li]What theories are of importance to analyzing this situation? (e.g. Grashoff?)[/li]
[li]Will the spot welds be a limiting factor to the size of P?[/li]
[li]How would you go about analyzing this scenario, if both the displacements and P_yield is of importance?[/li]
[li]How do you calculate the max value of P?[/li]
[/ul]
The scenario left me curious, as I have barely any idea how to answer his question.
Two steel profiles are fitted into each other. Both are fixed to the support, but the beams are only connected to each other with spot welds at the beams' ends.

To me it looks as if the stresses from the outer profile must be transferred to the inner profile through the spot welds, which could reduce the load that the profiles can withstand.
[ul]
[li]What theories are of importance to analyzing this situation? (e.g. Grashoff?)[/li]
[li]Will the spot welds be a limiting factor to the size of P?[/li]
[li]How would you go about analyzing this scenario, if both the displacements and P_yield is of importance?[/li]
[li]How do you calculate the max value of P?[/li]
[/ul]
The scenario left me curious, as I have barely any idea how to answer his question.