Question Regarding Laterally Supported Steel Beams

[Ilovestructures]

Hi all!

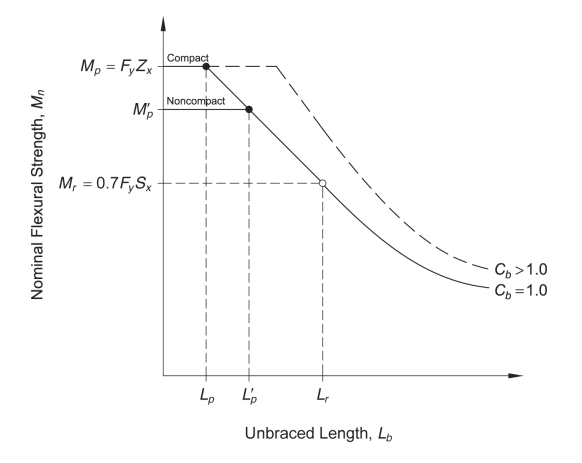
I'm taking my first course in steel design. I am struggling with understanding how to analyze flexural capacity for beams which we have to consider multiple segments or unbraced lengths. In general, do we just find the equivalent moment factor(Moment adjustment factor based on the moment diagram shape for that segment)and compute the capacity for each segment and then compare it with the MAXIMUM MOMENT IN THAT SEGMENT. If the computed resistance for that segment is greater than the MAX MOMENT IN THE SEGMENT, then that segment has adequate capacity, is this correct? or do we compute the resistance capacity for each segment and then take the lowest capacity as the one that governs for the entire beam. Please advise.

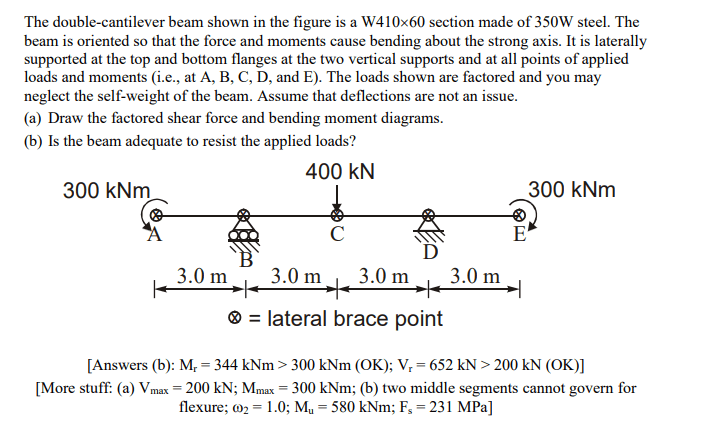
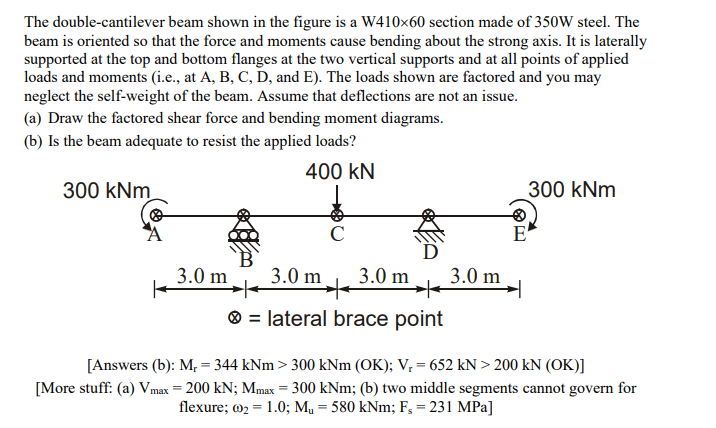
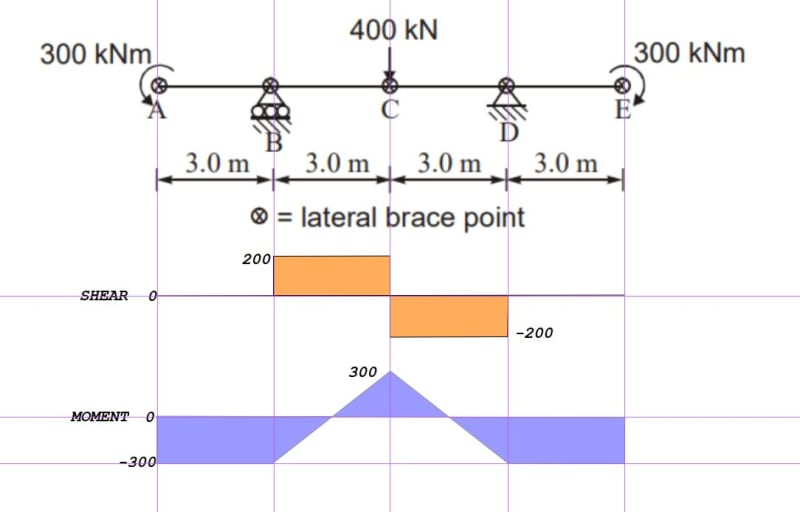
For example in this problem here, we have 4 unbraced segements to consider. Since it is symmetric we can only consider 2 segments. For Segment 1, Moment diagram is just a straight line and max moment is 300. factor is 1.0 . For the segment 2 max moment MAGNITUDE is also 300 but the moment factor is 2.39. we then get a higher capacity for segment 2. but for segment 1 our moment capacity is 234KNm and segmeent 2 is 347knm. Since the max moment IN SEGMENT 1 is 300 does that mean the beam does not adequatly resist the moment since its capacity for that segment is 234knm. Additionally how do we determine which segment governs the flexural capacity.

 

[BulbTheBuilder]

Let's assume a 10-metre-long beam braced laterally mid-span (5-metre).

The bending moment of the beam stays same (wl^2/8) with length being 10m. The unbraced length doesn't affect the bending the moment of the beam. However, the unbraced length affects the moment capacity.

How does it affect the moment capacity? As the unbraced length gets longer, there is a tendency for the beam to lateral/torsional buckle before the before the steel yields so the steel will still be in its elastic state.

Plastic strength>>>Elastic. To push the strength to the plastic limit, we reduce the unbraced length to achieve the plastic limit sate of the beam.

 

[271828]

If the computed resistance for that segment is greater than the MAX MOMENT IN THE SEGMENT, then that segment has adequate capacity, is this correct?

Almost. The resistance should be compared to the max moment in the segment that puts the potentially buckling flange in compression.

 

[271828]

In your example, the following is the moment diagram.

The interesting segment is between B and C. It has two LTB modes. You could call these Modes 1 and 2.

In Mode 1, the bottom flange buckles due to the negative moment between B and the inflection point (halfway between B and C). The max negative moment, at B, is the "demand" when you're checking this mode.

In Mode 2, the top flange buckles due to the positive moment between the inflection point and C. The max positive moment, at C, is the "demand" for this mode.

 

[BAretired]

Cantilevers AB and DE are the critical sections. According to the CISC handbook, a W410x60 has Mr=341kN-m at L=3000mm, so the W410x60 is adequate to resist the applied loads.

Since the max moment IN SEGMENT 1 is 300 does that mean the beam does not adequately resist the moment since its capacity for that segment is 234knm.

If that were true, that is precisely what it would mean, but I don't agree with the capacity of 234kN-m. Where did you get that figure?