Hello.
I guess someone here already did a PSV sizing according to the IGC flow requirements, see formulas below. The fire-factor is taken from table, L (latent heat), T, Z, M are all variables defined at relieving conditions of fluid to be relieved.
Could one explain how this can lead to the statement that the result Q is discharge of air at std. conditions and not of relieving fluid? Without further explanation it looks chaotic to me. Then, does density of air simply give a very conservative result for initial sizing?
In same paragraph it is refered to A.829 that comes up with a different formula for relieving flow under fire case, also shown below.
What I am doing is simply:
Q_gas_relief=Q_igc * (rho_gas_std / rho_gas_relief)
m_gas_relief=Q_gas_relief * rho_gas_relief
The results of this fit very good with the different formula from A.829 and also with the sizing software from PSV vendor.
From IGC:

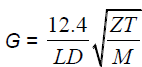

From A.829:

I guess someone here already did a PSV sizing according to the IGC flow requirements, see formulas below. The fire-factor is taken from table, L (latent heat), T, Z, M are all variables defined at relieving conditions of fluid to be relieved.
Could one explain how this can lead to the statement that the result Q is discharge of air at std. conditions and not of relieving fluid? Without further explanation it looks chaotic to me. Then, does density of air simply give a very conservative result for initial sizing?
In same paragraph it is refered to A.829 that comes up with a different formula for relieving flow under fire case, also shown below.
What I am doing is simply:
Q_gas_relief=Q_igc * (rho_gas_std / rho_gas_relief)
m_gas_relief=Q_gas_relief * rho_gas_relief
The results of this fit very good with the different formula from A.829 and also with the sizing software from PSV vendor.
From IGC:

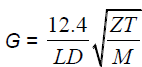

From A.829:

