Pile head moments in a simple bridge abutment model 3

[DimzK]

Good Evening,
I would like to ask a question about pile head moments in a simple bridge abutment model.
I have modeled two simple frame element models on SAP. The models are in longitudional direction and they look like this:

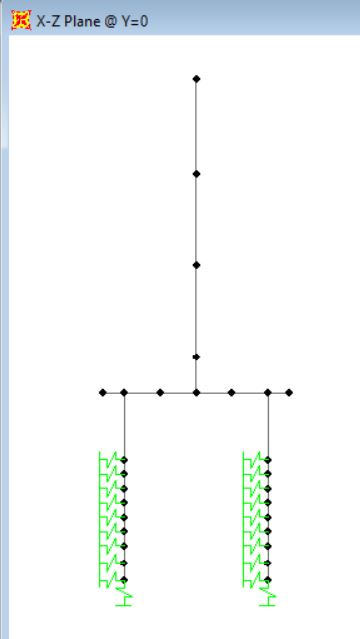
What both models have in common are:

1_ 4.5m design width
2_ Abutment stems are 2.5m x 4.5m
3_ Pile cap is 2.5m thick x 4.5m
4_ piles are 1.2m dia (2 piles per 4.5m design width)

The difference is:

1_Model 1 has 3.6m distance c/c between piles
2_ Model 2 has 5m distance c/c between piles.

The issue is I am getting vastly different Pile head moments for both models. I am trying to figure out why there are so vastly different. I know rotational stiffness (which takes length of frame in to account) will make some difference. But is it that much of a factor?

When I take away the soil springs and put fixed supports at the base of the piles, I get similar pile head moments for both models with only 100-200kNm difference. But when I introduce soil springs in to the model, the pile head moments vary greatly. I have checked the placement and vaules of the soil springs in both models and they are correct. So when there are soil springs, what causes the models to behave much differently and have huge difference in pile head moments?

Note: All below models do not have self weight.

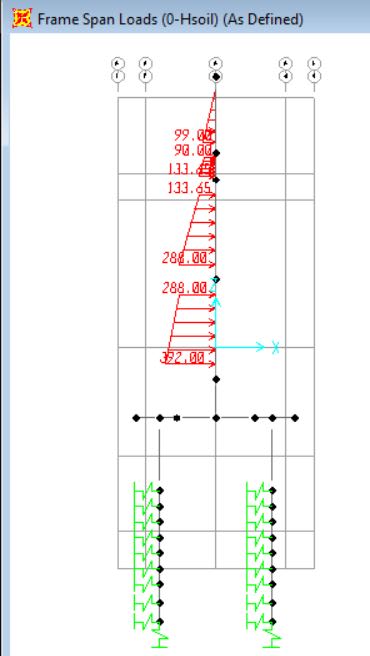
Below shows the two different models have the same soil loads on the stems:

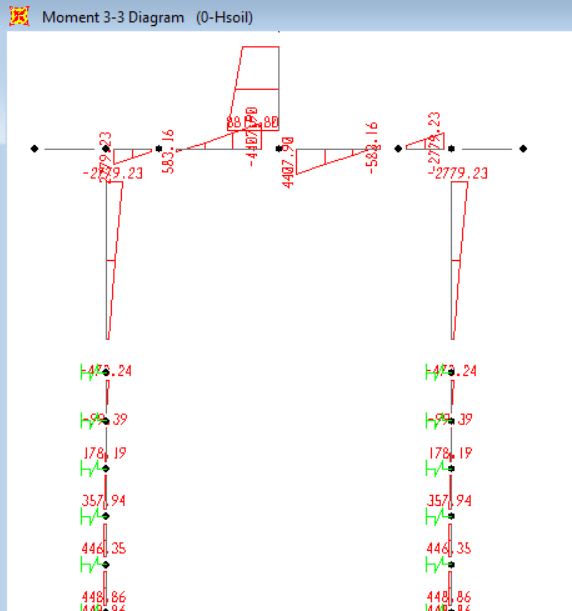
for 3.6m c/c model:

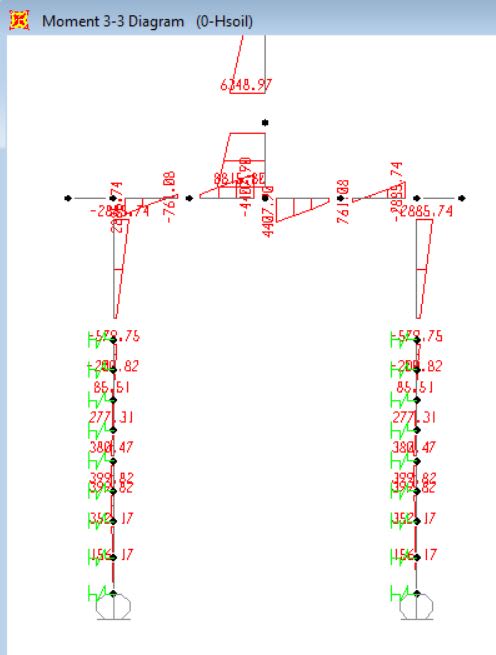
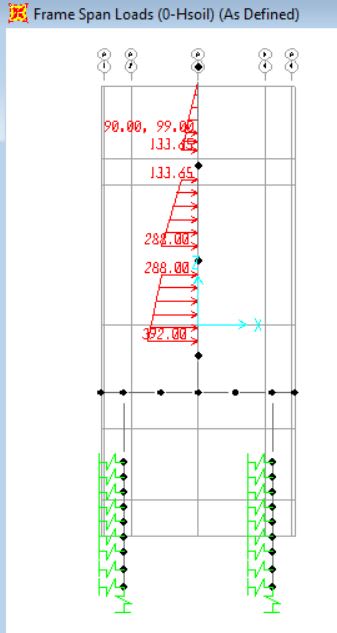
for 5m c/c model:

Shear though piles for 3.6m c/c model:

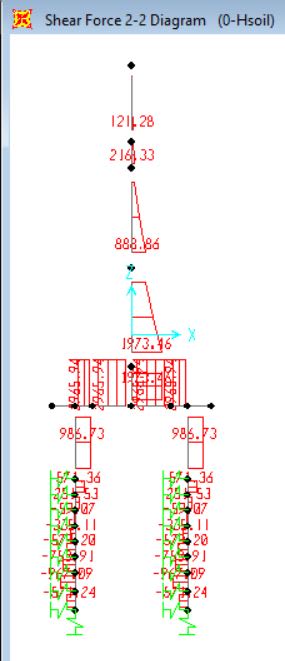
Shear through piles for 5m c/c model: (Note both has same pile shears)

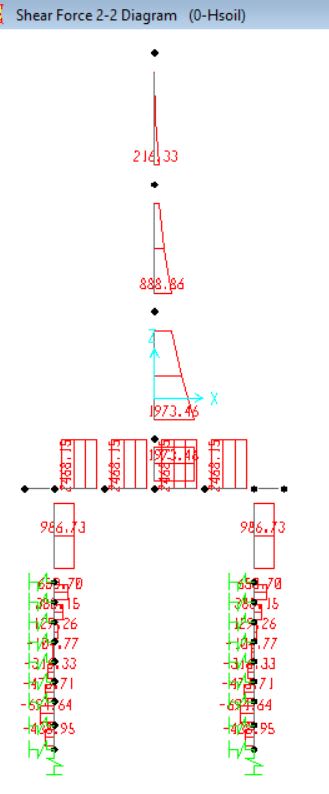
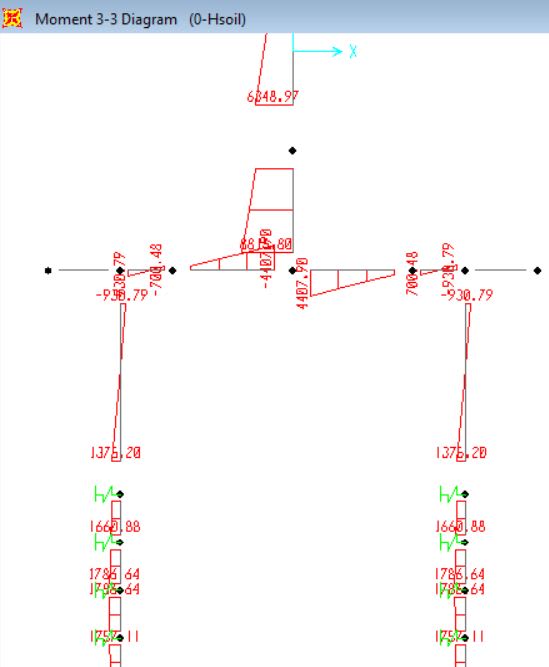
Moments for 3.6m model with springs: 930kNm pile head moment

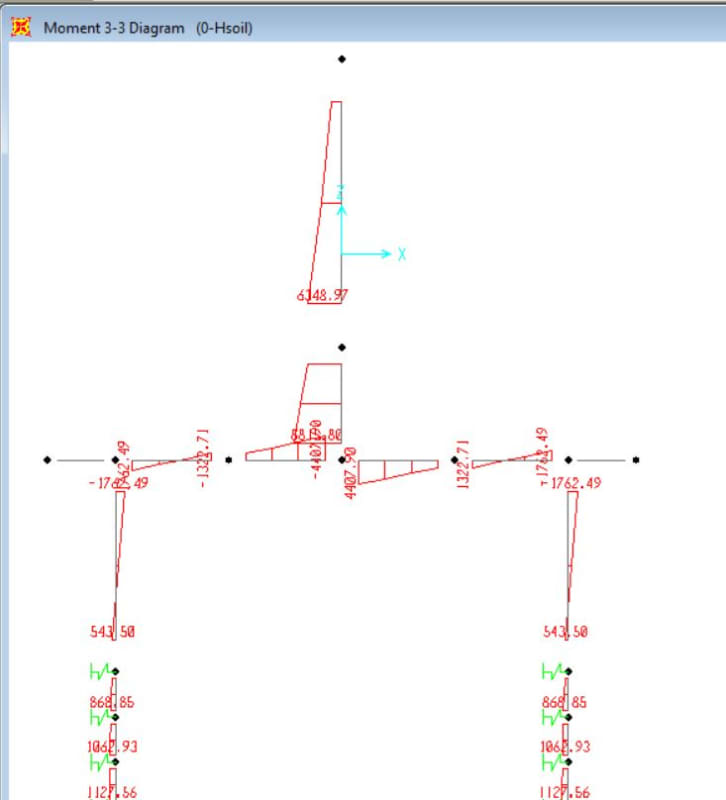
Moments for 5m model with springs: 1762kNm pile head moment

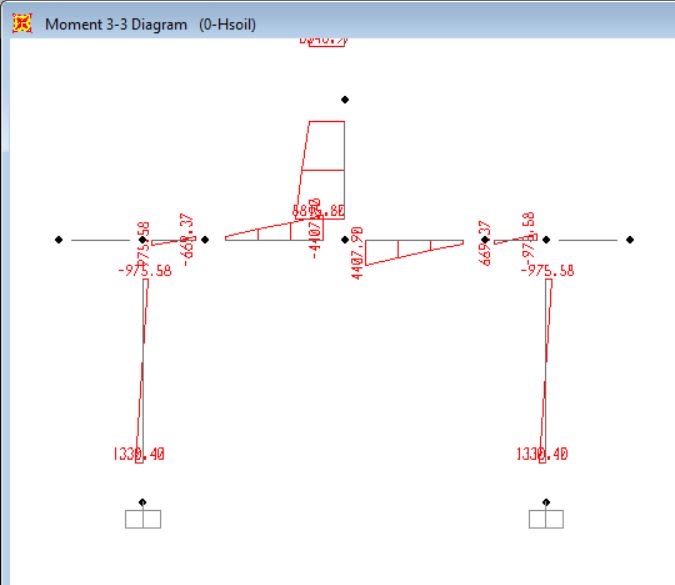
After supports fixed, with no springs, moments for 3.6m model: 3000kNm pile head moment

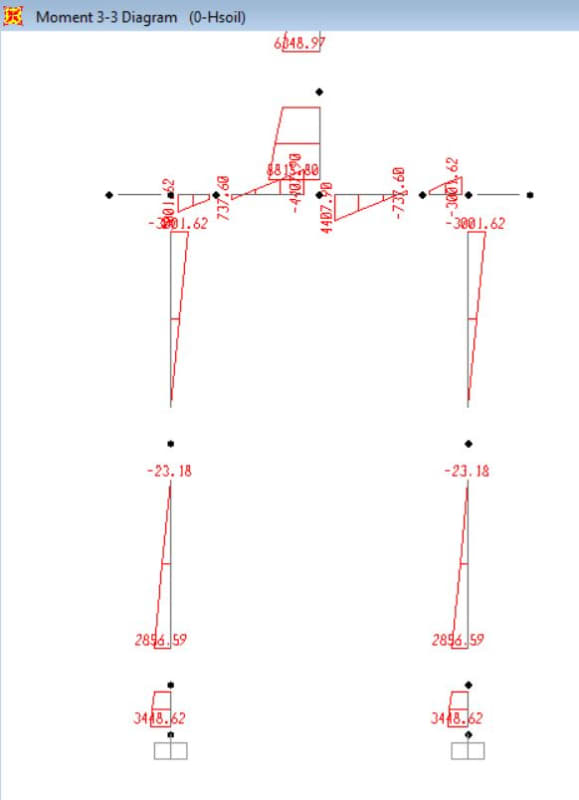
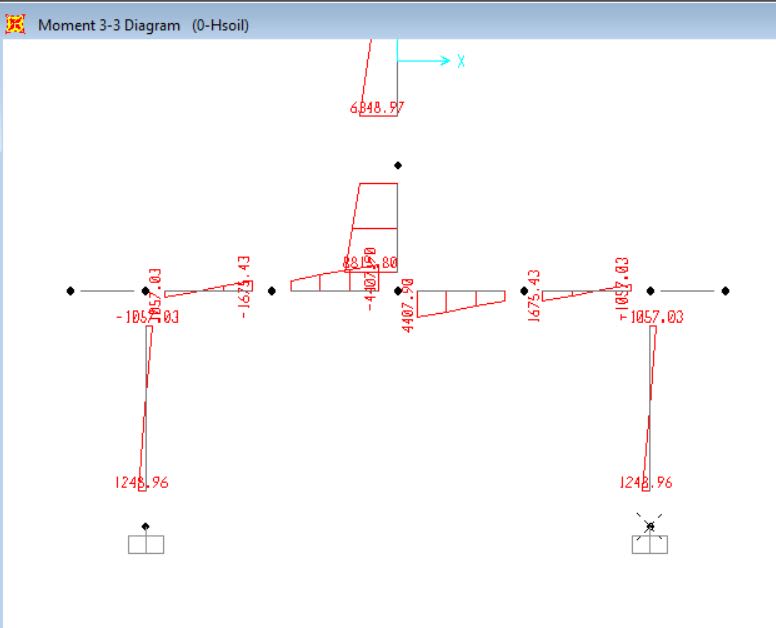
After supports fixed, moments for 5m model: 3100kNm pile head moment

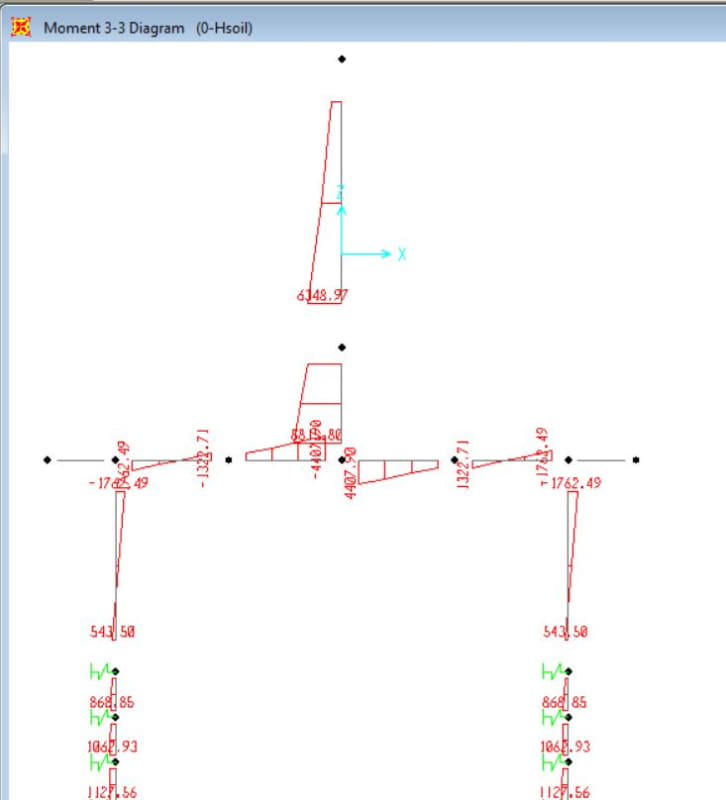
You can see, when supports are fixed, there is very little difference in pile head moment. When spring supports are introduced, the moment varies greatly (1762kNm vs. 930kNm). Why does this happen? Is this actually realistic? Thanks.

 

[Settingsun]

Looking at the shear force diagrams for the soil spring cases, immediately below the highest soil spring:
V = 571.36 kN for the 3.6m model
V = 659.70 kN for the 5.0m model.

This means that the reaction at the highest soil spring was greater in the 3.6m model (greater reduction in shear force), which means the 3.6m model deflected further horizontally at that point. It could just be that the greater deflection means the soil is giving better support to the 3.6m model, ie applying reaction forces closer to the applied loads.

I'd suggest the following route for investigation:
[ul]
[li]Delete the wall stem.[/li]
[li]Apply the horizontal load (1973.46 kN) and the moment (8815.80 kNm) as separate load cases, applied to the pile cap where the stem used to be.[/li]
[li]Try keeping the horizontal soil springs, but making the pile bases rigid vertically.[/li]
[li]Try other support conditions such as pinned bases and fixed bases (without the soil springs, but trying both vertically-rigid and vertically-sprung supports) to get some more insight into the model's behaviour.[/li]
[/ul]

The pile axial forces are greater for the 3.6m model, so the frame will rotate more due to the vertical pile springs. Making the piles rigid vertically will remove that source of deflection, which may even up the soil reactions and pile moments.

 

[DimzK]

Thank you for your response. When I roller support the vertical support at the bottom of the pile, I get similar moments=> 2779kNm for 3.6m vs 2885kNm for 5.0m.
From this It points to the fact that movement in the vertical direction is causing the moments to change at the pilehead. I am thinking that if I apply these movements as displacements to the model and check the moment generated by that, and minus from the moment generated by the pinned model, then If I get the answers I got in my original models as pile head moments, this would account for the difference in moments between the models.


Moment from 3.6m model with vertical roller support

Moment from 5m model with vertical roller support

Is there anyway I can check this with hand calculations? Moment distribution seems to be complicated when vertical and horizontal springs are involved.

 

[Ron]

Another approach you can take is determine the point of fixity for the piles and model the cantilever from there upward with little or no soil resistance.

 

[DimzK]

Hi Ron,

If I assume the upper most springs are the point of fixity and fix those points for both models, I get piled head moments of M=976kNm (c/c 3.6m) vs M=1057kNm (c/c = 5m).

What can you conclude from this? To me this seems to indicate that the springs are making a big difference in moment somehow. But I don't quite understand why as the springs have the same position and same stifness in both the models.

B= 3.6m

B=5m

 

[jayrod12]

I think what Ron was trying to indicate is determine at what point below the pilecap you reach fixity (or essentially fixity, I.e. point of zero shear) and then change your model to just fixed nodes at that location. See how that works out.

 

[ukbridge]

This is generally why you want to space your piles as far away as possible.

The behaviour of the system under an applied lateral load is essentially resisted as a combination of the following actions:

1) Push-pull action of the 2 piles (i.e. Force * lever arm / spacing of piles without the springs).
2) The beam on elastic foundation type behaviour of the piles on the soil springs.

Because you've effectively increased the lever arm by 50% its going to mainly fall under 1). When the spacing is less, the system resists the applied load and overturning moment mainly by the springs (their reactions will go up, and thus the moments in your pile will go up.) In your second model (with 5m spacing) the soil spring reactions should be a good chunk less.

All of this of course depends on the actual values of the springs you've assumed; its good practice (at least in my office) to half and double them and envelope the design effects especially if they've been established rather crudely. Its also a good idea to check the deflections and make sure they're not ridiculous, relative to the movement required to mobile passive pressures.

With the "fixed" model, you've basically introduced an infinitely stiff support - in that model you should find that the spring reactions along the pile are 0, while the base takes the lions share of the horizontal load.

Interesting problem! gl

 

[Settingsun]

I think the mechanism is that the tension and compression loads on the piles acting against the vertical springs at the pile bases cause the tension pile to move up and the compression pile to move down, which means rotation of the whole frame. The rotation means that the frame is moving further horizontally at the soil spring locations which generates larger reaction forces in the soil springs. This is reducing the effective bending length of the piles. Since the 3.6m frame has larger pile axial forces, this effect would be larger in the 3.6m frame, which did show smaller pile head moments in your initial analysis.

When you made the vertical springs rigid, the pile head moments increased significantly. So, following on from ukbridge's advice, you need to arrive at a comfortable set of values for the springs, especially the vertical springs. When thinking about that, bear in mind that vertical deflection of a pile is usually undesirable, so published stiffnesses may be underestimates, ie usually you'd want to calculate the maximum credible deflection. In your case, you want to know the minimum credible deflection. That would include shaft resistance as well as the base.