Modelling Footings using Springs 3

[StructuralAddict]

Hello everyone,

When idealising the supports of a building, we have three options:
1- Fixed Supports.
2- Pinned Supports.
3- Spring Supports with a defined rotational stiffness.

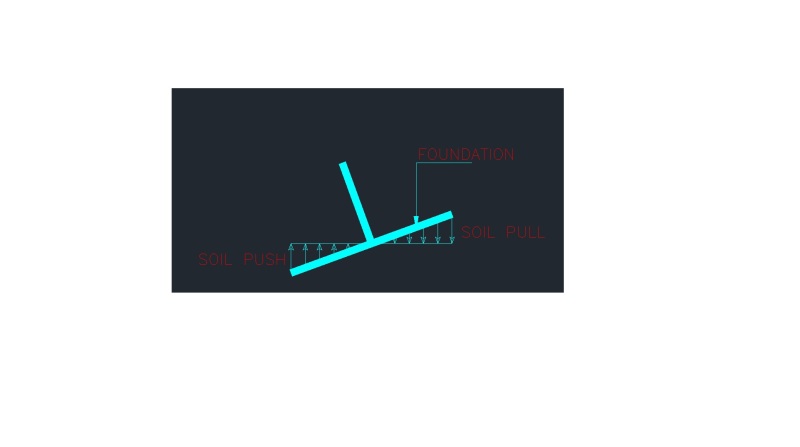
The attached file shows part of "Paulay and Priestley (1992)" book titled (Seismic Design of Reinforced Concrete and Masonry Buildings) discussing what is the most appropriate way to model foundations.

In summary, the footings can be best modelled by determining the flexural stiffness (K_f) of an equivalent spring. This can be calculated as:
(K_f) = (k_s)x(I_f)

where:
(k_s) is the subgrade modulus (MPa/m) and can be obtained easily from the soil report.
(I_f) is the (moment of inertia of the footing) divided by (soil interface corresponding with footing rotation).

Unfortunately, I am not sure of how to calculate the (If) factor in the above equation. I appreciate if anyone can provide me with a sample calculation for an arbitrary footing.

Thanks in advance!

 

[KootK]

Given a footing with plan dimensions B X H, I believe that I_f = BH^3/12

I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[StructuralAddict]

Thank you KootK, the equation that you provided is for the (moment of inertia of the footing). But what about the (soil interface corresponding with footing rotation)? how do we calculate this term?

Remember that: (I_f) is the (moment of inertia of the footing) divided by (soil interface corresponding with footing rotation).

 

[JoshPlumSE]

rotational stiffness = kip ft of moment per radian of rotation

Therefore, just calculate the moment that would develop if you imposed 1 radian of rotation on a footing with B and H dimensions resting on soil with a subgrade modulus of ks.

For simplicity, I would assume that the footing rotates about its centroid and that the resistance in tension is equal to the resistance in compression. The real behavior is more complicated, but it is also non-linear. And, we are only looking for a linear soil spring, right?

 

[KootK]

You're most welcome Monir87.

But what about the (soil interface corresponding with footing rotation)? how do we calculate this term?

I stand by my original recommendation. Consider it in terms of dimensional consistency. If you do it my way, you'll end up with:

k x I_f = MPa/m x m^4 = MN/m^3 X m^4 = MN*m = MN*m / Radians = Moment / unit rotation = Just what you want for a rotational spring stiffness. The rotation being unit-less of course. If you divided I_f by the interface area somehow, the units would no longer make sense.

Remember that: (If) is the (moment of inertia of the footing) divided by (soil interface corresponding with footing rotation)

In the referenced text "footing pad / soil interface" means "footing pad TO soil interface" not "footing pad DIVIDED by soil interface". Could that be the source of your confusion?


I like to debate structural engineering theory -- a lot. If I challenge you on something, know that I'm doing so because I respect your opinion enough to either change it or adopt it.

 

[StructuralAddict]

Thank you very much KootK and JoshPlum for your great explanations!
This made the calculation procedure easy to perform

 

[Shu Jiang PEng SE]

It seems that the formula be derived per the assumption that soil can apply both "push" and "pull" pressure on the foundation.

Assume foundation LxB, soil sub-grade modulus K, foundation rotate "A" under moment "M".

Maximum linear compressive pressure 1/2xL/2xAxKxB

Resultant of the compressive force on foundation 1/2x(1/2xL/2xAxKxB)xL/2=1/8xL^2xAxKxB

Moment to the foundation center due to compressive force (1/8xL^2xAxKxB)x2/3x(L/2)=1/24xBxL^3*KxA

The rotation stiffness of the half foundation 1/2xIxK. The soil can "pull" the foundation then the rotation stiffness is IxK.

My question is: Is the assumption acceptable?

 

[JasonMcKee71]

jiang46602, yes this is acceptable,but it can only be applied when the footing dims are relatively small so that it can be considered as a rigid body.

Jason McKee
proud R&D Manager of
Cross Section Analysis & Design
Software for the structural design of cross sections
Moment Curvature Analysis
Interaction Diagrams
Reifnorcement Design etc.

 

[Shu Jiang PEng SE]

JasonMcKee71.

I agree that the foundation should be treated as rigid. My point is that the foundation rotation stiffness is derived per the assumption that the soil can both "push" and "pull" the foundation when it rotates, as shown in the picture. My previous post showed how to derived the foundation rotation stiffness per the assumption.

The reality is that the soil can only "push" the foundation when the foundation moves toward the soil, and the soil has no restraints on the foundation when the foundation moves away from the soil. Therefore, the rotation stiffness derived per the assumption may be not appropriate.