I have a 43" dia x 1.5" thick disk sitting on top of an 8" dia shaft. I need to figure out how much the disk is going to flex downwards like an umbrella. Specifically the deflection amount on the OD edge. The only calculations I can find are for rupture disks and discs with the OD supported and how much deflection there is in the center. It can't be totally uncommon.
Navigation
Install the app
How to install the app on iOS
Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
More options
Style variation
-
Congratulations TugboatEng on being selected by the Eng-Tips community for having the most helpful posts in the forums last week. Way to Go!
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
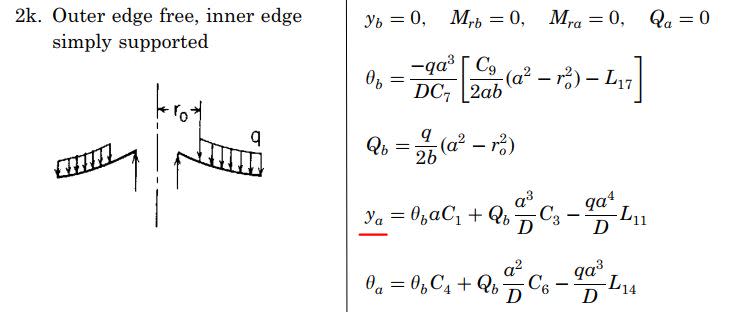
Large Disk Supported in Center - Deflection 2
- Thread starter CarbonCAD
- Start date
- Status
- Not open for further replies.
-
1
- #3
You'll find the formulas in Roark's. Note that you may have to superimpose one or more load cases. Specifically, if you use the load cases where the outside edge is simply supported, and superimpose load cases such that the outside reaction is zero, you then have a "free" edge condition.
- Thread starter
- #4
Deflection under it's own weight.
I'm thinking I may be able to use this from Roark's:
2. An annular aluminum plate with an outer radius of 20 in and an inner
radius of 5 in is to be loaded with an annular line load of 40 lb=in at a radius of
10 in. Both the inner and outer edges are simply supported, and it is required
to determine the maximum deflection and maximum stress as a function of the
plate thickness.
Once my plate starts to deflect it should act similar to a ring simply supported on the inner radius.
I'm thinking I may be able to use this from Roark's:
2. An annular aluminum plate with an outer radius of 20 in and an inner
radius of 5 in is to be loaded with an annular line load of 40 lb=in at a radius of
10 in. Both the inner and outer edges are simply supported, and it is required
to determine the maximum deflection and maximum stress as a function of the
plate thickness.
Once my plate starts to deflect it should act similar to a ring simply supported on the inner radius.
- Thread starter
- #5
according to your description (2. An annular aluminum plate with an outer radius of 20 in and an inner
radius of 5 in is to be loaded with an annular line load of 40 lb=in at a radius of
10 in. Both the inner and outer edges are simply supported, and it is required
to determine the maximum deflection and maximum stress as a function of the
plate thickness) should be Table 11.2 case no. 1k.
case no. 2k is for its own weight with "ro" equal to the inner radius
radius of 5 in is to be loaded with an annular line load of 40 lb=in at a radius of
10 in. Both the inner and outer edges are simply supported, and it is required
to determine the maximum deflection and maximum stress as a function of the
plate thickness) should be Table 11.2 case no. 1k.
case no. 2k is for its own weight with "ro" equal to the inner radius
Roark's 7th ed - table 11.2 - case 1k outer edge free, inner edge simply supported : the difference is the load. OP says annular line load of 40 lb=in at a radius of 10 in (exactly the case 1k)
In case 2k (as per OP) the load is not annular line load but uniformly distributed (own weight)
In case 2k (as per OP) the load is not annular line load but uniformly distributed (own weight)
LiftDivergence
Aerospace
How is the plate attached to the 8" dia. shaft?
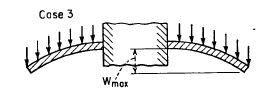
If you have a copy of Theory of Plates and Shells by Timoshenko, Chapter 3, Symmetrical Bending of Circular Plates, Case 3 on Page 62 might do well for you. That is for a case where a central column of material passes through the plate, but the boundary conditions may approximate your scenario better than the Roark Case above. Timoshenko's case basically assumes there is no deflection in the center where the disk is common to the shaft. That could be pretty close to what you have, depending on the attachment.
Keep em' Flying
//Fight Corrosion!
If you have a copy of Theory of Plates and Shells by Timoshenko, Chapter 3, Symmetrical Bending of Circular Plates, Case 3 on Page 62 might do well for you. That is for a case where a central column of material passes through the plate, but the boundary conditions may approximate your scenario better than the Roark Case above. Timoshenko's case basically assumes there is no deflection in the center where the disk is common to the shaft. That could be pretty close to what you have, depending on the attachment.

Keep em' Flying
//Fight Corrosion!
- Thread starter
- #13
Timoshenko was simpler and the solution I got was very close to what the average of the physical measurements. The problem with the physical measurements is that, in my case, it does not make a perfect "umbrella" but becomes wavy like a boonie hat brim. Very small and not visible by the naked eye but seen on the probe measurements.
-
1
- #14
- Status
- Not open for further replies.
Similar threads
- Replies
- 11
- Views
- 3K
- Question
- Replies
- 11
- Views
- 5K
- Locked
- Replies
- 3
- Views
- 5K
- Locked
- Question
- Replies
- 9
- Views
- 701
- Locked
- Question
- Replies
- 17
- Views
- 1K