odc53
Chemical
- Oct 11, 2015
- 1
Hello,
I am trying to calculate the cool down time of a stagnant fluid in an insulated pipe exposed to ambient winter conditions. I was wondering if the "lumped capacitance" method is the right approach to solve a problem like this?
The link: provides the following equation to calculate the cool down time:
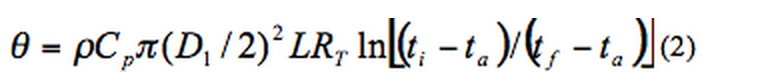
Where:
Theta = cooling time
RT = insulation heat transfer coefficient
The equation above looks much the same as the solution to a lumped capacitance problem, however, the convective heat transfer coefficient, H, is being replaced with the the thermal resistance of the insulation, RT. My question is whether it is appropriate to do so? The insulation itself will have a temperature gradient which will vary over time, and this equation doesn't seem to account for that (atleast that is my understanding).
If anyone can shed some light on this topic that would be great.
I am trying to calculate the cool down time of a stagnant fluid in an insulated pipe exposed to ambient winter conditions. I was wondering if the "lumped capacitance" method is the right approach to solve a problem like this?
The link: provides the following equation to calculate the cool down time:
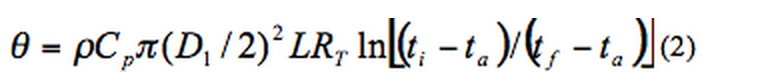
Where:
Theta = cooling time
RT = insulation heat transfer coefficient
The equation above looks much the same as the solution to a lumped capacitance problem, however, the convective heat transfer coefficient, H, is being replaced with the the thermal resistance of the insulation, RT. My question is whether it is appropriate to do so? The insulation itself will have a temperature gradient which will vary over time, and this equation doesn't seem to account for that (atleast that is my understanding).
If anyone can shed some light on this topic that would be great.
