Hi everyone!
I'm new here and just registered since I thought this might be a good place to ask.
I'm an aeronautics engineer specialized in the fields of thermodynamics and fluid mechanics, currently working as a researchers.
This is also the reason why I feel quite stupid having to ask this question...![[bigsmile] [bigsmile] [bigsmile]](/data/assets/smilies/bigsmile.gif) But I've been dealing with so many equations now, out of which this task is by far the easiest, but still got my brain completely confused on such a basic problem...
But I've been dealing with so many equations now, out of which this task is by far the easiest, but still got my brain completely confused on such a basic problem...
I want to calculate the heat content of a thermal energy storage, filled with water (liquid, no phase change). With this heat content I want to evaluate the state-of-charge of the TES. Thus I have a set of current temperatures, a set of lowest temperatures and a set of highest temperatures.
Let's simplify by dividing the storage in 3 control volumes of which I've got the temperatures. The total volume is V=1m^3. Material properties cp and rho are also quite exact in the range from 0°C to 100°C.
Now I've got three states (temperatures top to bottom):
- fully charged, temperatures, state "max": T_max = [90, 70, 50] °C
- fully discharged, temp. , state "min": T_min = [70, 30, 10] °C
- partly charged, temp. , state "now": T_now = [80, 60, 30] °C
edit: Forgot to mention that it is an "open" storage, thus mass may change due to changes in density.
To get the heat content, I'd go with
Q = sum(T * cp(T) * rho(T) * V_cell)
for all three states (charged, disch., partly ch.) with V_cell = V / 3
And then to get the remaining SOC to max/min:
SOC_max = Q_max - Q_now
SOC_min = Q_now - Q_min
BUT... I need to integrate over cp and rho between the current state and a reference state. (or at least take the mean).
And this is where I'm getting stuck. Since I need to "precalculate" the max/min heat content Q, I can't integrate, since at the point where I calculate "now"-state, I have no information about the min/max temperatures.
What should I do? The options I have considered so far:
[ul]
[li] Calculate Q with reference 0°C for all three states "max/min/now": Q = sum(T * (cp(T) + cp(0°C))/2 * (rho(T) + rho(0°C))/2 * V_cell) (currently preferred)[/li]
[li] Calculate Q with reference 0°C while on the Kelvin scale for all three states "max/min/now": Q = sum((T + 273.15) * (cp(T) + cp(0°C))/2 * (rho(T) + rho(0°C))/2 * V_cell)[/li]
[li] Calculate Q without reference for all three states "max/min/now": Q = sum(T * cp(T) * rho(T) * V_cell)[/li]
[li] Calculate Q without reference on the Kelvin scale for all three states "max/min/now": Q = sum((T + 273.15) * cp(T) * rho(T) * V_cell)[/li]
[/ul]
I guess you all know that when you start thinking about basics too much, basics become the real problem... Thus I just had to ask this.
Thus I just had to ask this.
Many thanks in advance!
Best regards,
scooter
I'm new here and just registered since I thought this might be a good place to ask.
I'm an aeronautics engineer specialized in the fields of thermodynamics and fluid mechanics, currently working as a researchers.
This is also the reason why I feel quite stupid having to ask this question...
![[bigsmile] [bigsmile] [bigsmile]](/data/assets/smilies/bigsmile.gif) But I've been dealing with so many equations now, out of which this task is by far the easiest, but still got my brain completely confused on such a basic problem...
But I've been dealing with so many equations now, out of which this task is by far the easiest, but still got my brain completely confused on such a basic problem...I want to calculate the heat content of a thermal energy storage, filled with water (liquid, no phase change). With this heat content I want to evaluate the state-of-charge of the TES. Thus I have a set of current temperatures, a set of lowest temperatures and a set of highest temperatures.
Let's simplify by dividing the storage in 3 control volumes of which I've got the temperatures. The total volume is V=1m^3. Material properties cp and rho are also quite exact in the range from 0°C to 100°C.
Now I've got three states (temperatures top to bottom):
- fully charged, temperatures, state "max": T_max = [90, 70, 50] °C
- fully discharged, temp. , state "min": T_min = [70, 30, 10] °C
- partly charged, temp. , state "now": T_now = [80, 60, 30] °C
edit: Forgot to mention that it is an "open" storage, thus mass may change due to changes in density.
To get the heat content, I'd go with
Q = sum(T * cp(T) * rho(T) * V_cell)
for all three states (charged, disch., partly ch.) with V_cell = V / 3
And then to get the remaining SOC to max/min:
SOC_max = Q_max - Q_now
SOC_min = Q_now - Q_min
BUT... I need to integrate over cp and rho between the current state and a reference state. (or at least take the mean).
And this is where I'm getting stuck. Since I need to "precalculate" the max/min heat content Q, I can't integrate, since at the point where I calculate "now"-state, I have no information about the min/max temperatures.
What should I do? The options I have considered so far:
[ul]
[li] Calculate Q with reference 0°C for all three states "max/min/now": Q = sum(T * (cp(T) + cp(0°C))/2 * (rho(T) + rho(0°C))/2 * V_cell) (currently preferred)[/li]
[li] Calculate Q with reference 0°C while on the Kelvin scale for all three states "max/min/now": Q = sum((T + 273.15) * (cp(T) + cp(0°C))/2 * (rho(T) + rho(0°C))/2 * V_cell)[/li]
[li] Calculate Q without reference for all three states "max/min/now": Q = sum(T * cp(T) * rho(T) * V_cell)[/li]
[li] Calculate Q without reference on the Kelvin scale for all three states "max/min/now": Q = sum((T + 273.15) * cp(T) * rho(T) * V_cell)[/li]
[/ul]
I guess you all know that when you start thinking about basics too much, basics become the real problem...
Many thanks in advance!
Best regards,
scooter

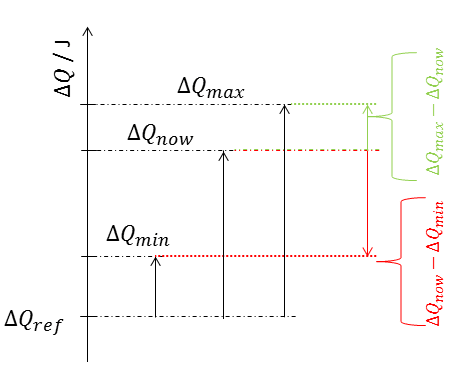
![[glasses] [glasses] [glasses]](/data/assets/smilies/glasses.gif) So it's going the be the first way, using ref. temperature 0°C.
So it's going the be the first way, using ref. temperature 0°C.