SKJ25POL
Structural
- Mar 4, 2011
- 358
I like to get some opinions on the correct degree of indeterminacy of below frame?
Thank you
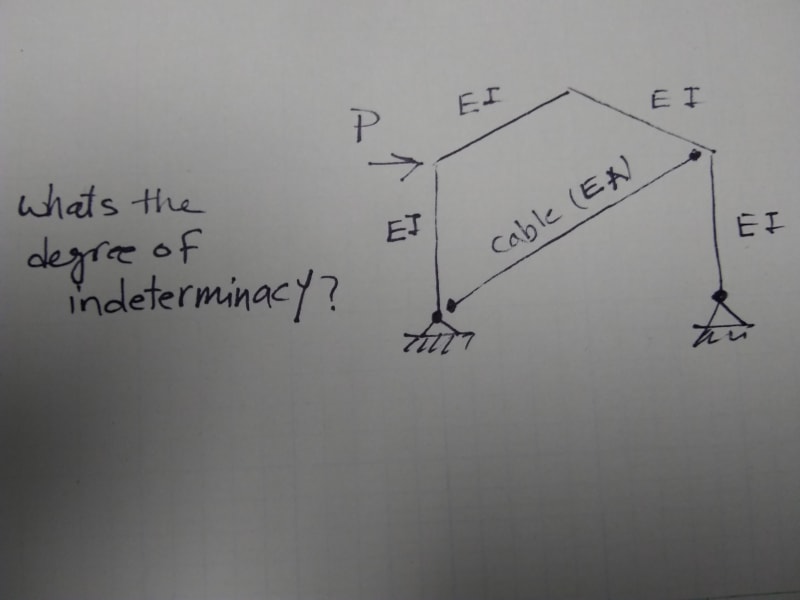
Thank you

Follow along with the video below to see how to install our site as a web app on your home screen.
Note: This feature may not be available in some browsers.
Jayrod said:Unstable to a point, that diagonal brace would restrain it quite well if you ask me. at least for loading applied towards the right of the page.
