Ball/Cylindrical object rolling down incline 1

[WARose]

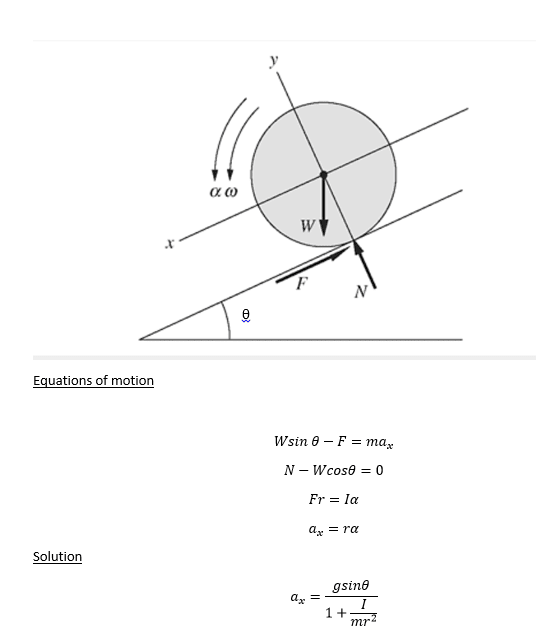
If you'll note, this is marked as a "tip" thread....I've been doing a lot of bin design lately....and I had to go back into the old dynamics book to consider some scenarios.....one of them is a ball or cylinder rolling down a incline (without slipping)....I.e. what velocity (relative to it's center) will develop for rolling (without slipping) if it is released from rest on a incline? So here goes:

V_ball=[(10/7)*g*L*SinΘ]^1/2

V_cylinder=[(4/3)*g*L*SinΘ]^1/2

where:

V=velocity [in distance/second]
g=gravitational acceleration
L=rolling distance on incline (starting from release)
Θ=angle of the incline (off the horizontal)

It actually took a while to figure out....so I thought I'd post for the future thread searches for interested parties.

Interesting the subtle difference (based on the different inertias) for the two different shapes.

Thanks for reading.

 

[dik]

Interesting that the radius/diameter has no effect.... thanks for posting...

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[MacGyverS2000]

I'm reminded of Statics class many moons ago where the following (paraphrased) question was posed: "Imagine a yo-yo on the ground with it's string, half unrolled, extended parallel to the ground. The string is pulled away from the yo-yo. In which direction does the yo-yo rotate?"

The math makes it obvious, but (general human, non-engineering trained) common sense alone really muddles the issue. I love that kind of stuff...

Dan - Owner

http://www.Hi-TecDesigns.com

 

[3DDave]

Now do it for a Brachistchrone path.

As an amusing aside - there's an interactive museum nearby that installed package rollers as a slide. They are in the form of a cylinder a couple of inches in diameter and five feet long. The rollers are set so closely that fingers can't get nipped. The fun is watching parents putting their little kids on it. The children progress down at a stately pace. Then the parents climb aboard and go by at a near perilous pace. It's a wonderful physics demonstration.

 

[WARose]

Interesting that the radius/diameter has no effect....

IIRC it was a variable in the inertia formula.....but it cancelled out (at some point)....so did the mass (which surprised me).

 

[goutam_freelance]

Actually the mass center will have an acceleration. But according to your formula velocity is constant.

Engineers, think what we have done to the environment !

https://www.linkedin.com/in/goutam-das-59743b30/

 

[dik]

or an epicycloid path...

Rather than think climate change and the corona virus as science, think of it as the wrath of God. Feel any better?

-Dik

 

[HTURKAK]

Yes...the inertia is the only variable.. regarding the mass, it does not effect the free fall velocity remember, v=SQRT(g*H)...

For this case V=SQRT( a*L) L = sloped surface travelled. if you put the acceleration at Mr. goutam_freelance 's post, you will get the velocities for sphere and cylinder..

 

[goutam_freelance]

Oh ! I did not notice that L is a variable. Usually we use lowercase for variables ( except T K). Anyway formula given by OP is correct.

Engineers, think what we have done to the environment !

https://www.linkedin.com/in/goutam-das-59743b30/

 

[WARose]

Oh ! I did not notice that L is a variable. Usually we use lowercase for variables ( except T K). Anyway formula given by OP is correct.

Oh I know I am correct.....after all, one of my answers matched the answer in the back of the book! (And that can't be wrong....right? )

Too bad the answers were only for the odd numbered problems. (In this case, the ball velocity was confirmed.)