eli28
Aerospace
- Oct 20, 2019
- 109
hello everybody,
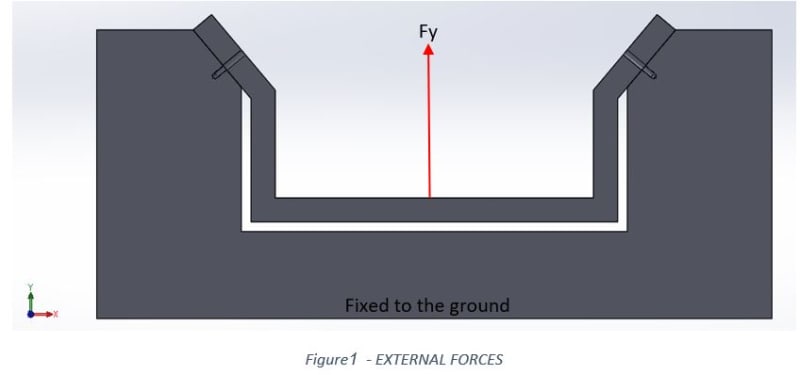
I graduated long ago, and I am trying to figure out how to calculate reactions in bolted joint, so I will be able to know what is the external tensile load on each bolt and in addition the shear force that is actually the outcome of a friction generated by the pressure the bolt exerts.
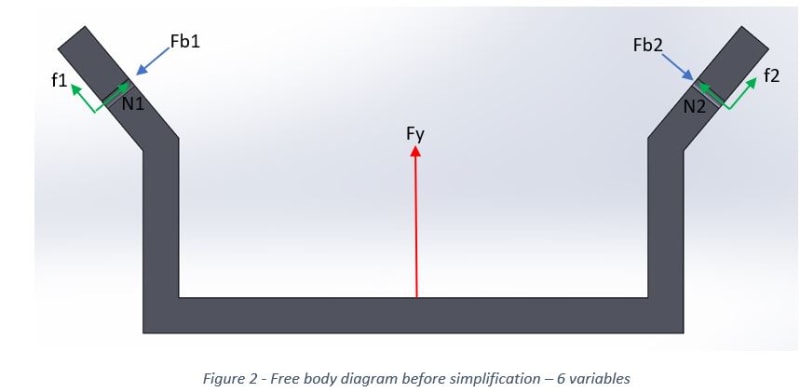
I am trying to draw a free body diagram of a quite simple problem, but I find it difficult to solve since there are only 3 equations and 4 unknowns.
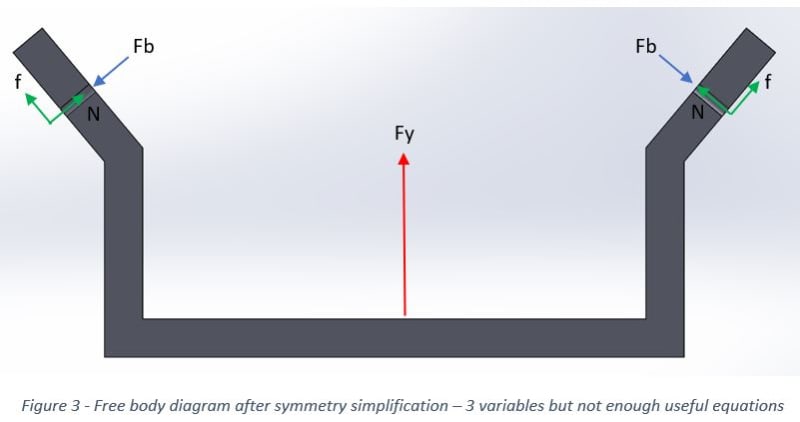
when I try to assume that as a result of symmetry the right reactions = left reactions I get a contradiction while formulating the equilibrium equation in the X direction.
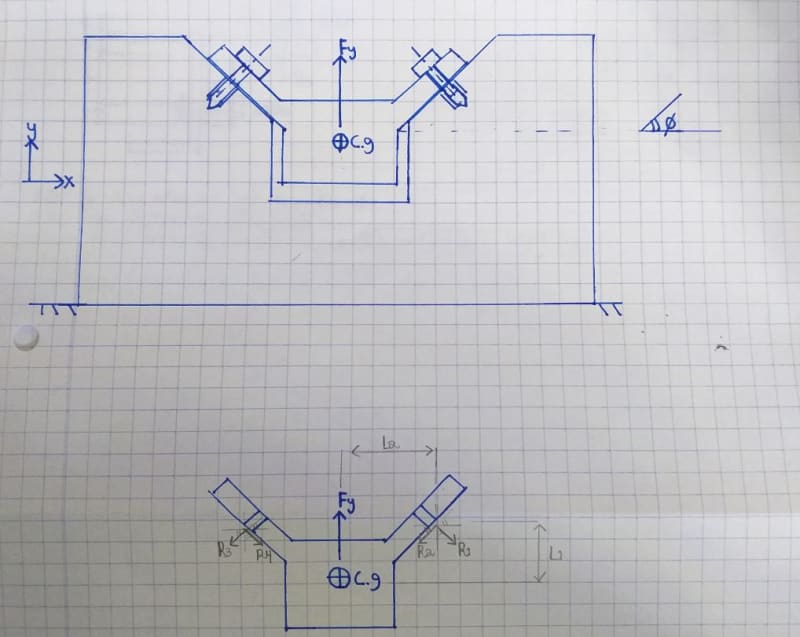
I graduated long ago, and I am trying to figure out how to calculate reactions in bolted joint, so I will be able to know what is the external tensile load on each bolt and in addition the shear force that is actually the outcome of a friction generated by the pressure the bolt exerts.
I am trying to draw a free body diagram of a quite simple problem, but I find it difficult to solve since there are only 3 equations and 4 unknowns.
when I try to assume that as a result of symmetry the right reactions = left reactions I get a contradiction while formulating the equilibrium equation in the X direction.


![[smile2] [smile2] [smile2]](/data/assets/smilies/smile2.gif)