Calculating moment for a beam with a tapered load on part of the span

DTS419 · Tuesday at 8:42 PM

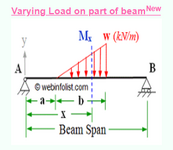
I'm looking for a beam formula to calculate the bending moment for a beam with a tapered load on only part of the span. Every reference book I have has the same beam formulas which include a beam with a tapered load on the entire span, but none where the tapered load is only applied to part of the span. Think basement wall that is pinned top and bottom and has a backfill load at some height above the base or something like this...

ChorasDen · Tuesday at 8:47 PM

Have you tried figuring it out by using methods of cuts or virtual work?

DTS419 · Tuesday at 8:51 PM

Tough to do by hand because the shear is not linear so the area of the shear diagram is tough to determine. It can easily be done in Enercalc but I am looking for a simple formula I can put in a spreadsheet like the many scenarios that are shown in most beam formula tables.

Celt83 · Tuesday at 9:00 PM

Direct integration from the piecewise formulas I find best suited for spreadsheet entry. I would recommend solving this for the trapezoidal load case that way you will end up with formulas that cover uniform loads, triangular loads, and trapezoidal loads.

For the trapezoidal load case you'll have 12 integration constants to solve for using the various boundary and compatibility formulas.

you can use your CAS software of choice to aid solving it symbolically, I like wxmaxima as it's free, https://wxmaxima-developers.github.io/wxmaxima/.

ChorasDen · Tuesday at 9:08 PM

Here is what I came up with in 5 minutes, after having to retrain myself on the method. I give no guarantees of the formulas though, but from a quick glance they seem appropriate.

DTS419 · Tuesday at 9:10 PM

Celt83 said:
Direct integration from the piecewise formulas I find best suited for spreadsheet entry. I would recommend solving this for the trapezoidal load case that way you will end up with formulas that cover uniform loads, triangular loads, and trapezoidal loads.

For the trapezoidal load case you'll have 12 integration constants to solve for using the various boundary and compatibility formulas.

you can use your CAS software of choice to aid solving it symbolically, I like wxmaxima as it's free, https://wxmaxima-developers.github.io/wxmaxima/.

I thought about that, but I haven't done integration in 20+ years. I am hoping someone out there has a reference table that provides an algebraic formula for max moment.

ChorasDen · Tuesday at 9:16 PM

you still need to compute the reactions based on my equations, but that should be trivial for any typical design case. I'll summarize here for readability:

1) For x >= (A+B)
Mc = RD*l - (WB(l-x))/2

2) For x<=A
Mc = l*RE-(WB(l-x))/2

3) For A < x < (A+B)
Mc = RD*l-(l-x)(w(l-A)/2)

refer to the drawing to try and decipher what each variable is indicating, note that x and l change based on the detail.

ChorasDen · Tuesday at 9:18 PM

DTS419 said:
Tough to do by hand because the shear is not linear so the area of the shear diagram is tough to determine. It can easily be done in Enercalc but I am looking for a simple formula I can put in a spreadsheet like the many scenarios that are shown in most beam formula tables.

It's trivial to do by methods of cuts. Simply take a cut in the member where you wish to know the moment, and calculate the moments around that location. You can do the same thing to derive M = WL^2/8 when x=L/2 for a uniformly loaded member if you desire.

EngDM · Tuesday at 9:26 PM

Here is the derivation of uniformly distributed load. I believe it belongs to @Celt83 and it works piecewise for any UDL magnitude, location, etc. Principles of superposition can be used for multiple loads. Have it solve for maximize M while varying X, and then have it maximize deflection while varying X (not always the same X for deflection and moment maximums). I've used this and back checked it with software. The equations are LONG, so if you have an error, check your equations.

Edit: Removed the link. I noticed @Celt83 replied to this thread and did not provide it themselves, not sure if they want it public anymore.

IDS · 2025-08-06T01:30:38+0100

Alternative formulas giving shear, moment and deflection at any point, from The Reinforced Concrete Designer's Handbook (Reynolds and Steedman):

For spreadsheets providing shear, moment, slope and deflection for any number of point or trapezoidal loads on cantilever, single span, or multiple spans with any end conditions see:

https://newtonexcelbach.com/2023/01/20/using-conbeamu/

or for the Python version:

https://newtonexcelbach.com/2024/08/28/py_conbeam-5/

271828 · 2025-08-06T02:45:55+0100

I got the following by:
1. Write equations for the reactions at each end.
2. Cut a section to the left of the load. Sum moments to get M1.
3. Cut a section within the load. Sum moments to get M2.
4. Cut a section to the right of the load. Sum moments to get M3.

I checked three cases relative to SAP2000 or AISC Table 3-22 Case 2, and got the same answers.

SE2607 · 2025-08-06T03:05:11+0100

DTS419 said:
I thought about that, but I haven't done integration in 20+ years. I am hoping someone out there has a reference table that provides an algebraic formula for max moment.

Integration of this problem is easy-peasy. The integral of Axⁿ=Axⁿ⁺¹/(n+1)+B

Eng-Tips is the largest forum for Engineering Professionals on the Internet.

Members share and learn making Eng-Tips Forums the best source of engineering information on the Internet!

Calculating moment for a beam with a tapered load on part of the span

DTS419

Structural

ChorasDen

Structural

DTS419

Structural

Celt83

Structural

ChorasDen

Structural

DTS419

Structural

ChorasDen

Structural

ChorasDen

Structural

EngDM

Structural

IDS

Civil/Environmental

271828

Structural

SE2607

Structural

Similar threads

Part and Inventory Search

Sponsor