rockman7892
Electrical
- Apr 7, 2008
- 1,178
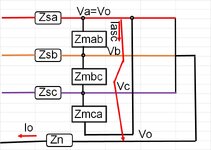
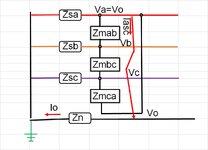
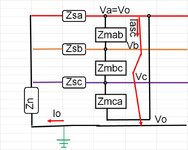
I know that for a single L-G fault the ground fault current If on the faulted phase is represented as 3I0 and it is this 3I0 that can be measured and represented as ground fault current. I also understand that this 3I0 value comes from the contribution of both the pos sequence, neg sequence and zero sequence current on the faulted phase (I1=I2=I0=1/3IF).
What I am not clear on however is what if any zero sequence is present in the other two unfaulted phases during a L-G fault. I recall reading somewhere once that there is I0 current in the other two phases however they are offset by the negative sequence current in those phases?
If there is I0 current present in the other un-faulted phases can it be measured with CT/relaying on that phase or is it offset to the degree where it is not measurable?
Appreciate any insight in helping my understanding.
What I am not clear on however is what if any zero sequence is present in the other two unfaulted phases during a L-G fault. I recall reading somewhere once that there is I0 current in the other two phases however they are offset by the negative sequence current in those phases?
If there is I0 current present in the other un-faulted phases can it be measured with CT/relaying on that phase or is it offset to the degree where it is not measurable?
Appreciate any insight in helping my understanding.