Creative Engineer:
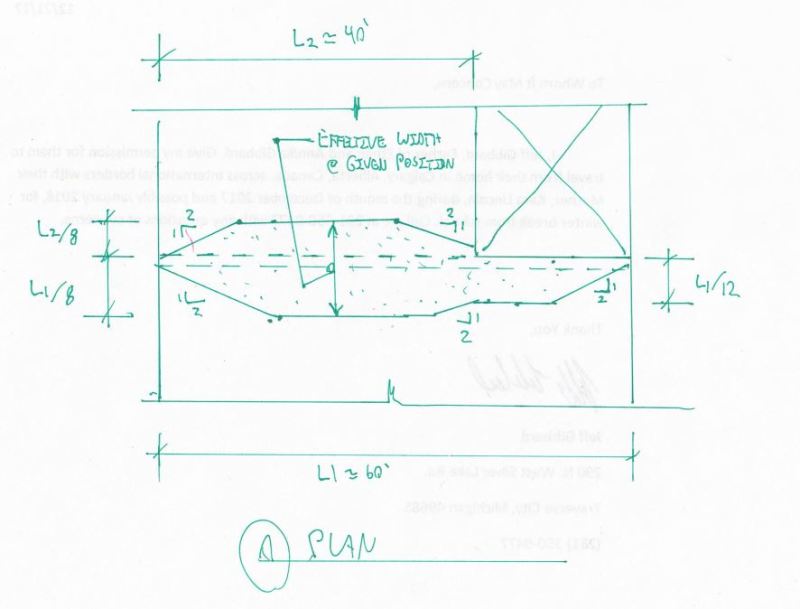
Effective flange width is a shear flow and shear lag phenomenon and as such, it is dependent upon beam length (span length) for its full (progressing) development. Thus, the longer beam can provide for more flange development, but this is somewhat self limiting too, and does not go on (linearly or otherwise) forever as the beam lengthens. The flg. (slab) stress is generally bell shaped with its max. over the beam and decreasing as you move further away from the beam, to some truncated value, as a function of the max. flg. stress you will allow. The flg. stress you use for design is some average of this bell curve, for simplicity of design. Furthermore, the phenomenon is highly dependant upon sudden changes in loads, concentrated loads and reactions (shear changes), and geometric changes. We can probably all grasp the basic problem, a uniformly loaded simple span beam, with the effective flange width growing from some small width at the reactions (beam ends) to some max. effective/practical width at midspan. But, any changes in loading or beam geometry really mess up that simplistic example problem. I don’t have the last few latest eds. of the ACI code so I don’t know exactly what those sections or the commentary say about the issue. But, I suspect it is somewhat empirical and conservative; the 1/4 (15', 7.5' each side for the ‘T’ bm.) and 1/12 (5' on one side for the ‘L’ bm.) values have been around for a long time. Like Rapt, I think I would use the full span length for both, since the phenomenon starts, and grows from the beam ends, but realize, that at the 41' location, and a number of feet on either side of it, you will have an indeterminate stress picture in terms of how the two effective widths (actual slab stresses) blend together. Rapt has probably studied this problem in some detail, I haven’t. I would also add some rebars, in the slab, at the reentrant slab corner. With the computer power and software you have now, I suspect you don’t really need this ‘effective width’ design simplification any longer to have a far better stress picture than we ever had, with a hand held calculator.