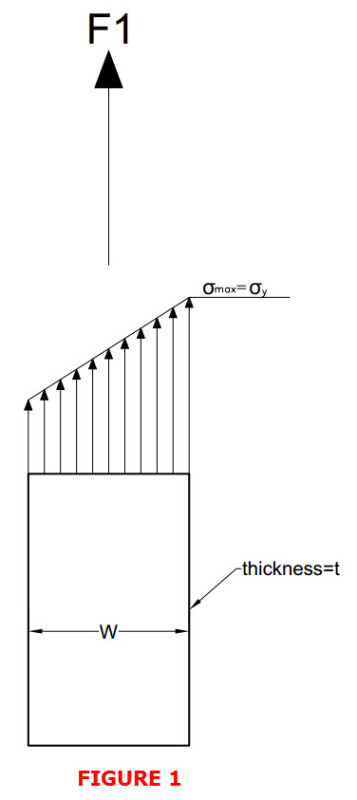
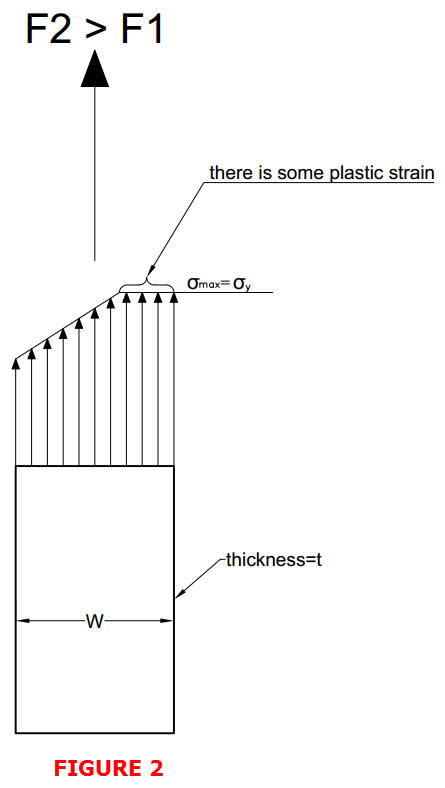
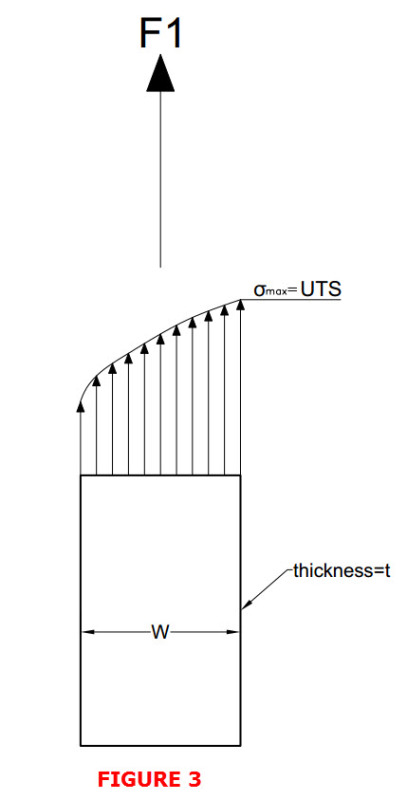
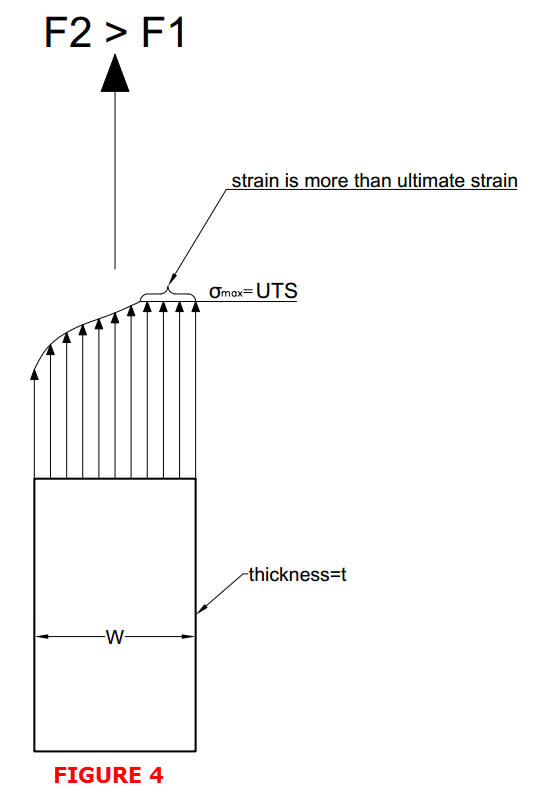
Hi,
I`ve started some reading on Elastic-Plastic analysis, according to ASME VIII-2 Part 5. I still have a long path to go, but my first question is about which is the more suitable model of hardening to use?
On ASME PTB-3, I saw that Prager hardening is used on ABAQUS software, unfortunately I only have access to ANSYS, on Workbench, from what I saw I have basically two options of hardening models to use: Multilinear isotropic hardening and Multilinear Kinematic hardening (there are some other methods but they use different inputs than stress and strain).
From my searchs, the difference between them is basically the Bauschinger effect, but I`m not quite sure on its application.
PS: For this study of mine, I`m dealing with only with static loads.
Thanks for the attention
I`ve started some reading on Elastic-Plastic analysis, according to ASME VIII-2 Part 5. I still have a long path to go, but my first question is about which is the more suitable model of hardening to use?
On ASME PTB-3, I saw that Prager hardening is used on ABAQUS software, unfortunately I only have access to ANSYS, on Workbench, from what I saw I have basically two options of hardening models to use: Multilinear isotropic hardening and Multilinear Kinematic hardening (there are some other methods but they use different inputs than stress and strain).
From my searchs, the difference between them is basically the Bauschinger effect, but I`m not quite sure on its application.
PS: For this study of mine, I`m dealing with only with static loads.
Thanks for the attention