mechengineer
Mechanical
For easy to see the difference, we may use the same allowable stress S=138 MPa for both formulas in VIII-1 and VIII-2.
VIII-1 formula: t1=PRi/(SE-0.6Pi)
Maximum principal strength theory is applied. The stress intensity equals a hoop stress and assume it is consistent along the wall thickness.
VIII-2 formula: t2=Ri[exp(Pi/SE)-1], [VIII-1 Appendix 1-2 formula (1) is same as VIII-2 formula]
Maximum shear strength theory (Tresca criterion) is applied. It is considered as 2-direction stress state, hoop stress and longitudinal stress. And assume that a radial stress is zero.
Conditions given:
1. Vessel ID=1000 mm
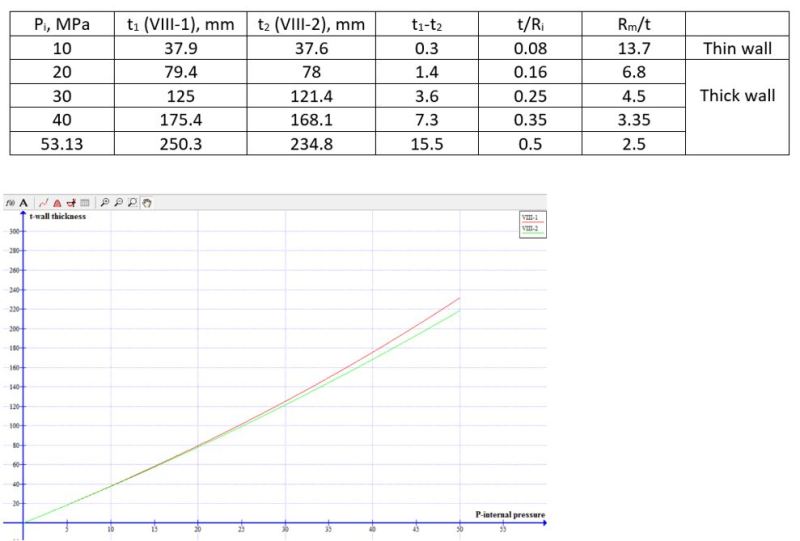
2. Design pressure Pi see the table below (0.385*S=53.13, limit of VIII-1 formula)
3. Allowable stress S=138 MPa
4. Joint efficiency E=1
5. Rm – vessel mean radius
Calculation results, comparison table and curve are shown in the end of last program.
Discussion on the comparison table:
1. When the safety factor is not considered, although the two formulas of VIII-1 and VIII-2 are very different in form and different in strength theory, the calculation results are almost same especially in case of the thin wall vessel (Rm/t≥10) or design pressure P≤20 MPa.
2. Question: Why does not ASME code update to use a single formula with respective individual safety factor, like the code case 2695? Any reason in behind to keep the two different formulas with a same result calculated (excluding the influence of safety factor)? No matter what strength theories are applied, but the results are almost same. It looks like that does not make sense for the stress analysis and make people confused. Welcome comment on this point.
VIII-1 formula: t1=PRi/(SE-0.6Pi)
Maximum principal strength theory is applied. The stress intensity equals a hoop stress and assume it is consistent along the wall thickness.
VIII-2 formula: t2=Ri[exp(Pi/SE)-1], [VIII-1 Appendix 1-2 formula (1) is same as VIII-2 formula]
Maximum shear strength theory (Tresca criterion) is applied. It is considered as 2-direction stress state, hoop stress and longitudinal stress. And assume that a radial stress is zero.
Conditions given:
1. Vessel ID=1000 mm
2. Design pressure Pi see the table below (0.385*S=53.13, limit of VIII-1 formula)
3. Allowable stress S=138 MPa
4. Joint efficiency E=1
5. Rm – vessel mean radius
Calculation results, comparison table and curve are shown in the end of last program.
Discussion on the comparison table:
1. When the safety factor is not considered, although the two formulas of VIII-1 and VIII-2 are very different in form and different in strength theory, the calculation results are almost same especially in case of the thin wall vessel (Rm/t≥10) or design pressure P≤20 MPa.
2. Question: Why does not ASME code update to use a single formula with respective individual safety factor, like the code case 2695? Any reason in behind to keep the two different formulas with a same result calculated (excluding the influence of safety factor)? No matter what strength theories are applied, but the results are almost same. It looks like that does not make sense for the stress analysis and make people confused. Welcome comment on this point.

