Good morning
We have a 20 m high retaining wall with a 4x4 m footing seating right beside the edge of the retaining wall. How can I estimate an equivalent lateral force (and its location) on the wall caused by the footing? I've been thinking of two approaches so far but I am not sure if are they appropriate.
I was thinking of using a simplified 2:1 (slope) load distribution approach to estimate vertical pressure at any given depth and to convert this vertical pressure into lateral one by multiplying it by Ka.
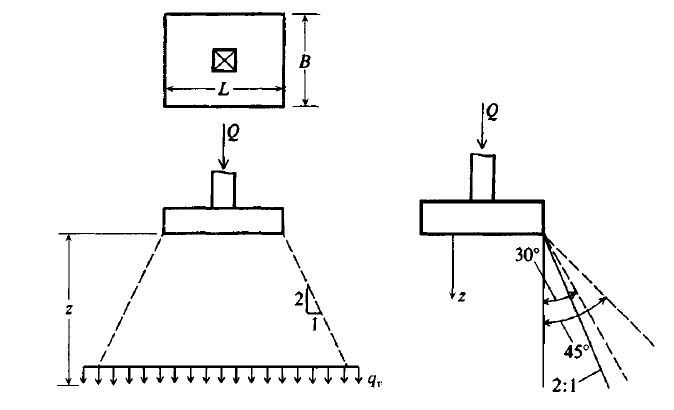
The problem is the higher the wall the higher the equivalent lateral force. At certain wall height the equivalent lateral force becomes bigger than the original vertical force on the footing which I guess does not really sound logical.
The second approach I was thinking of is the one suggested by Bowles (1992) to use theory of elasticity (The Boussinesq Equation for point load) to estimate the lateral pressure. Bowles suggested to divide a square load into many point loads and to calculate a lateral contribution of each at the certain depth. So theoretically I can calculate a lateral force distribution with the depth. The problem is again this lateral distribution (similar to stress bulbs) won't be constant everywhere but will keep changing along the edge of the footing (and away from it).
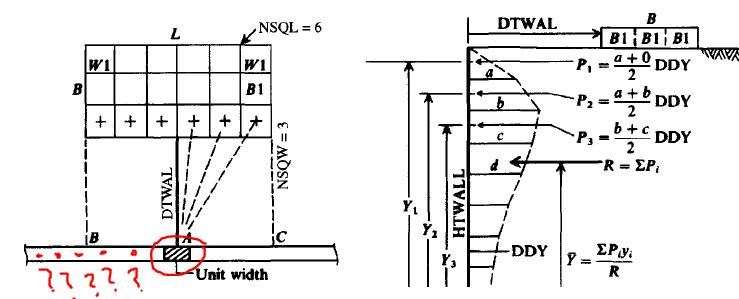
So I have to do some sort of integration on all these lateral distributions. This makes it very hard to come up with an equivalent lateral force.
My other option would probably be using one of these 3D FE programs.
Am I out of options or missing something?
Would appreciate your advice.
Thank you
We have a 20 m high retaining wall with a 4x4 m footing seating right beside the edge of the retaining wall. How can I estimate an equivalent lateral force (and its location) on the wall caused by the footing? I've been thinking of two approaches so far but I am not sure if are they appropriate.
I was thinking of using a simplified 2:1 (slope) load distribution approach to estimate vertical pressure at any given depth and to convert this vertical pressure into lateral one by multiplying it by Ka.

The problem is the higher the wall the higher the equivalent lateral force. At certain wall height the equivalent lateral force becomes bigger than the original vertical force on the footing which I guess does not really sound logical.
The second approach I was thinking of is the one suggested by Bowles (1992) to use theory of elasticity (The Boussinesq Equation for point load) to estimate the lateral pressure. Bowles suggested to divide a square load into many point loads and to calculate a lateral contribution of each at the certain depth. So theoretically I can calculate a lateral force distribution with the depth. The problem is again this lateral distribution (similar to stress bulbs) won't be constant everywhere but will keep changing along the edge of the footing (and away from it).

So I have to do some sort of integration on all these lateral distributions. This makes it very hard to come up with an equivalent lateral force.
My other option would probably be using one of these 3D FE programs.
Am I out of options or missing something?
Would appreciate your advice.
Thank you
