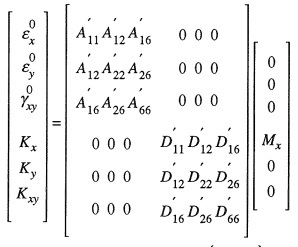fernandosalvador
Mechanical
Good evening friends,
Suppose I have a square plate (2" x 2"), of a carbon/epoxy laminate, for instance with 4 layers: [0,+45]s, where one edge is fixed, and in the opposite edge, a transverse load (say, in the Z direction) of 1000 lb is applied, producing a bending. (pretty much like a cantilever beam, I guess)
|
|
_________ v
/| |
/| |
/|_________|
I'm trying to figure our how can I perform a analytical stress analysis of the laminate with these boundary conditions neglecting moisture and thermal effects.
I tried to use the CLT with a moment Mx of 500 lb/in/in but seems that this approach is wrong, since the transverse load of 1000 lb will induce a non-uniform moment, and also a shear stress (?), which I don't know how to represent in the calculations.
In order to be clear, my first main goal here is to determine the strains and stresses along each ply (top/bottom). And plot a graph of the stresses trough the thickness.
Is the Classical Laminate Theory enough to predict those results?
I have those books that might help:
"An introduction to composite materials" - Hull (1st ed)
"Introduction to composite materials design" - Barbero (1st ed)
However I'm still in the beginning of the course here in US, I have 20 years old, and English is my second language, so I'm still struggling to find this answer on those books.
I really appreciate your attention, and I'm looking forward to get some answers to extend my knowledge and hopefully be able to improve my community. Thanks.
Fernando.
Suppose I have a square plate (2" x 2"), of a carbon/epoxy laminate, for instance with 4 layers: [0,+45]s, where one edge is fixed, and in the opposite edge, a transverse load (say, in the Z direction) of 1000 lb is applied, producing a bending. (pretty much like a cantilever beam, I guess)
|
|
_________ v
/| |
/| |
/|_________|
I'm trying to figure our how can I perform a analytical stress analysis of the laminate with these boundary conditions neglecting moisture and thermal effects.
I tried to use the CLT with a moment Mx of 500 lb/in/in but seems that this approach is wrong, since the transverse load of 1000 lb will induce a non-uniform moment, and also a shear stress (?), which I don't know how to represent in the calculations.
In order to be clear, my first main goal here is to determine the strains and stresses along each ply (top/bottom). And plot a graph of the stresses trough the thickness.
Is the Classical Laminate Theory enough to predict those results?
I have those books that might help:
"An introduction to composite materials" - Hull (1st ed)
"Introduction to composite materials design" - Barbero (1st ed)
However I'm still in the beginning of the course here in US, I have 20 years old, and English is my second language, so I'm still struggling to find this answer on those books.
I really appreciate your attention, and I'm looking forward to get some answers to extend my knowledge and hopefully be able to improve my community. Thanks.
Fernando.