All,
When have you guys ever reduced Vuc to 0 by adopting the following clause?

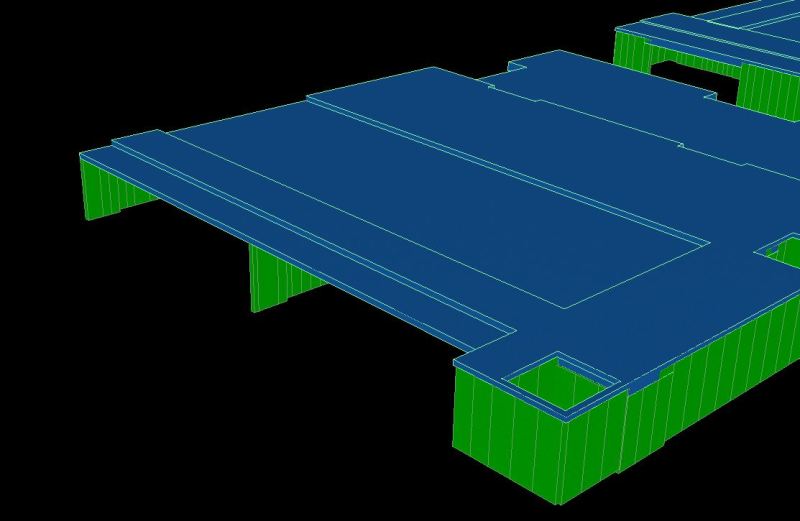
My situation: compatibility torsion on an internal T beam, from elastic uncracked analysis, is higher than 0.25PhiTuc and thus requires transverse steel to resist this torsion.
Now this torsion could potentially cause cracks (45 deg to long. axis) in the compression zone of the section and thus why I'm wondering whether to ignore the concrete contribution in shear?
Ignoring this moment and assuming cracking/redistribution of load to the adjacent slabs has occurred also leads me to believe that Vuc should be 0.
When have you guys ever reduced Vuc to 0 by adopting the following clause?

My situation: compatibility torsion on an internal T beam, from elastic uncracked analysis, is higher than 0.25PhiTuc and thus requires transverse steel to resist this torsion.
Now this torsion could potentially cause cracks (45 deg to long. axis) in the compression zone of the section and thus why I'm wondering whether to ignore the concrete contribution in shear?
Ignoring this moment and assuming cracking/redistribution of load to the adjacent slabs has occurred also leads me to believe that Vuc should be 0.